
【题目】已知抛物线y= ![]() x2+1(如图所示).
x2+1(如图所示).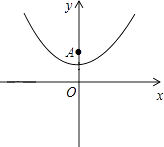
(1)填空:抛物线的顶点坐标是( , ),对称轴是;
(2)已知y轴上一点A(0,2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上.在平面内是否存在点N,使四边形OAMN为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由.
【答案】
(1)0;1;x=0(或y轴)
(2)
解:∵△PAB是等边三角形,
∴∠ABO=90°﹣60°=30°.
∴AB=20A=4.
∴PB=4.
解法一:把y=4代入y= ![]() x2+1,
x2+1,
得 x=±2 ![]() .
.
∴P1(2 ![]() ,4),P2(﹣2
,4),P2(﹣2 ![]() ,4).
,4).
解法二:∴OB= ![]() =2
=2 ![]()
∴P1(2 ![]() ,4).
,4).
根据抛物线的对称性,得P2(﹣2 ![]() ,4)
,4)
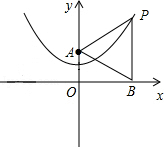
(3)
解:∵点A的坐标为(0,2),点P的坐标为(2 ![]() ,4)
,4)
∴设线段AP所在直线的解析式为y=kx+b
∴ ![]()
解得: 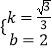
∴解析式为:y= ![]() x+2
x+2
设存在点N使得OAMN是菱形,
∵点M在直线AP上,
∴设点M的坐标为:(m, ![]() m+2)
m+2)
如图,作MQ⊥y轴于点Q,则MQ=m,AQ=OQ﹣OA= ![]() m+2﹣2=
m+2﹣2= ![]() m
m
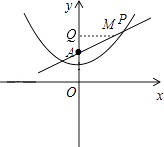
∵四边形OAMN为菱形,
∴AM=AO=2,
∴在直角三角形AMQ中,AQ2+MQ2=AM2,
即:m2+( ![]() m)2=22
m)2=22
解得:m=± ![]()
代入直线AP的解析式求得y=3或1,
当P点在抛物线的右支上时,分为两种情况:
当N在右图1位置时,
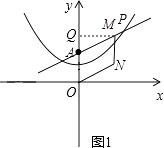
∵OA=MN,
∴MN=2,
又∵M点坐标为( ![]() ,3),
,3),
∴N点坐标为( ![]() ,1),即N1坐标为(
,1),即N1坐标为( ![]() ,1).
,1).
当N在右图2位置时,
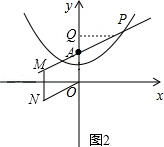
∵MN=OA=2,M点坐标为(﹣ ![]() ,1),
,1),
∴N点坐标为(﹣ ![]() ,﹣1),即N2坐标为(﹣
,﹣1),即N2坐标为(﹣ ![]() ,﹣1).
,﹣1).
当P点在抛物线的左支上时,分为两种情况:
第一种是当点M在线段PA上时(PA内部)我们求出N点坐标为(﹣ ![]() ,1);
,1);
第二种是当M点在PA的延长线上时(在第一象限)我们求出N点坐标为( ![]() ,﹣1)
,﹣1)
∴存在N1( ![]() ,1),N2(﹣
,1),N2(﹣ ![]() ,﹣1)N3(﹣
,﹣1)N3(﹣ ![]() ,1),N4(
,1),N4( ![]() ,﹣1)使得四边形OAMN是菱形
,﹣1)使得四边形OAMN是菱形
【解析】解:(1)顶点坐标是(0,1),对称轴是y轴(或x=O).
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某超市销售进价为2元的雪糕,在销售中发现,此商品的日销售单价x(元)与日销售量y(根)之间有如下关系:
日销售单价x(元) | 3 | 4 | 5 | 6 |
日销售量y(根) | 40 | 30 | 24 | 20 |
(1)猜测并确定y和x之间的函数关系式;
(2)设此商品销售利润为W,求W与x的函数关系式,若物价局规定此商品最高限价为10元/根,你是否能求出商品日销售最大利润?若能请求出,不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD(AD>AB)中,将它折叠,使点A与C重合,折痕EF交AD于E,交BC于F,交AC于O,连结AF、CE. 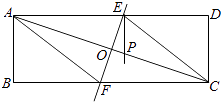
(1)求证:四边形AFCE是菱形;
(2)过E作EP⊥AD交AC于P,求证:AE2=AOAP;
(3)若AE=8,△ABF的面积为9,求AB+BF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年1月,由于雾霾天气持续笼罩我国中东部大部分地区,口罩市场出现热卖,某旗舰网店用8000元购进甲、乙两种口罩,销售完后共获利2800元,进价和售价如下表:
品名 | 甲种口罩 | 乙种口罩 |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该网店购进甲、乙两种口罩各多少袋?
(2)该网店第二次以原价购进甲、乙、两种口罩,购进乙种口罩袋数不变,而购进甲种口罩袋数是第一次的2倍.甲种口罩按原售价出售,而乙种口罩让利销售.若两种口罩销售完毕,要使第二次销售活动获利不少于3680元,乙种口罩最低售价为每袋多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.

(1)在图1中以格点为顶点画一个面积为5的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、![]() ;
;
(3)如图3,A、B、C是小正方形的顶点,求∠ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.

(1)求证:四边形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四边形AODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了数据的收集、整理与描述后,为妈妈整理记录了10月份的家庭支出情况,并绘制成如下尚不完整的统计图表,请你根据图表信息完成下列各题:
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | 400 |
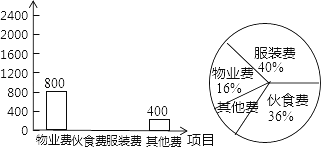
(1)10月份小明家共支出多少元?
(2)在扇形统计图中,表示“其他费”的扇形圆心角为多少度?
(3)请将表格补充完整;
项目 | 物业费 | 伙食费 | 服装费 | 其他费 |
金额/元 | 800 | ________ | ________ | 400 |
(4)请将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
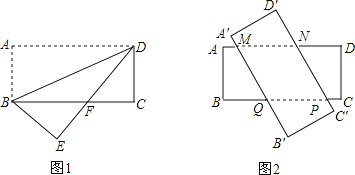
【题目】有两张相同的矩形纸片ABCD和A′B′C′D′,其中AB=3,BC=8.
(1)若将其中一张矩形纸片ABCD沿着BD折叠,点A落在点E处(如图1),设DE与BC相交于点F,求BF的长;
(2)若将这两张矩形纸片交叉叠放(如图2),判断四边形MNPQ的形状,并证明.四边形MNPQ的最大面积是_________.(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com