
【题目】某农户准备围建一个矩形苗圃园,其中一边靠墙,另外三边用30米长的篱笆围成,已知墙长为18米,设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若垂直于墙的一边为多少米时,苗圃园的面积最大值?最大面积是多少?
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
![]()
【答案】(1)x=12;(2)S最大=112.5(3)6≤x≤10.
【解析】试题分析:
(1)由题意结合图形可列出方程:x(30-2x)=72,结合0<![]() 即可求得x的值;
即可求得x的值;
(2)设苗圃的面积为S,则由题意可得S= ![]() ,结合
,结合![]() 可知,当
可知,当![]() 时,S最大=
时,S最大=![]() ;
;
(3)由x(30﹣2x)=100解得x1=5,x2=10,结合二次函数S=x(30﹣2x)的图象开口向下,且x≥6即可得到:当S>100时,x的取值范围是6≤x≤10.
试题解析:
(1)根据题意得:(30﹣2x)x=72,
解得:x=3,x=12,
∵30﹣2x≤18,
∴x=12;
(2)依题意得0<30﹣2x≤18所以,15>x≥6,
∵S=﹣2(x﹣![]() )2+
)2+![]() ,
,
由二次函数的性质可得:
当![]() 时,S最大=112.5
时,S最大=112.5
(3)令x(30﹣2x)=100,
即x2﹣15x+50=0,解得x=5或10,
因为S=x(30﹣2x)的图象开口向下,且x≥6,所以当这个苗圃的面积不小于100平方米时,x的取值范围是6≤x≤10.


科目:初中数学 来源: 题型:
【题目】![]() 为直线
为直线![]() 上一点,以
上一点,以![]() 为顶点作
为顶点作![]() ,射线
,射线![]() 平分
平分![]()
(1)如图①,![]() 与
与![]() 的数量关系为______
的数量关系为______

(2)如图①,如果![]() ,请你求出
,请你求出![]() 的度数并说明理由;
的度数并说明理由;
(3)若将图①中的![]() 绕点
绕点![]() 旋转至图②的位置,
旋转至图②的位置,![]() 依然平分
依然平分![]() ,若
,若![]() ,请直接写出
,请直接写出![]() 的度数
的度数

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直线y=﹣x沿y轴向下平移后的直线恰好经过点A(2,﹣4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
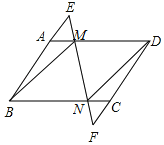
【题目】如图,已知平行四边形ABCD延长BA到点E,延长DC到点E,使得AE=CF,连结EF,分别交AD、BC于点M、N,连结BM,DN.
(1)求证:AM=CN;
(2)连结DE,若BE=DE,则四边形BMDN是什么特殊的四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表:

我们把某一格中所有字母相加得到的多项式称为特征多项式,例如:第1格的“特征多项式”为x+4y.
回答下列问题:
⑴ 第4格的“特征多项式”为 ,第n格的“特征多项式”为 ;
⑵ 若第1格的“特征多项式”的值为2,第2格的“特征多项式”的值为-6.
① 求x,y的值;
② 在①的条件下,第n格的“特征多项式的值”随着n的变化而变化,求“特征多项式的值”的最大值及此时n值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
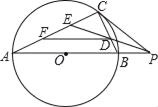
【题目】如图,AB为⊙O的直径,P为AB延长线上一点,PC与⊙O相切于点C,∠P的平分线交BC、AC于点D、E.则下列结论正确的结论有 (填序号)
(1)△PBC∽△PCA (2)△PCD∽△PAE
(3)△CDE是等腰直角三角形 (4)点E、F三等分AC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com