
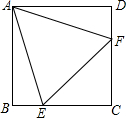
 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④AD=$\sqrt{3}$,其中正确的结论个数为( )
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④AD=$\sqrt{3}$,其中正确的结论个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据三角形的全等的知识可以判断①的正误;根据角角之间的数量关系,以及三角形内角和为180°判断②的正误;根据线段垂直平分线的知识可以判断③的正确;利用解三角形求正方形的面积等知识可以判断④的正误.
解答 解:∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{AE=AF}\end{array}\right.$,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC-BE=CD-DF,
∴CE=CF,
∴①说法正确;
∵CE=CF,
∴△ECF是等腰直角三角形,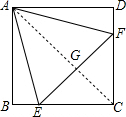
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,
∴②说法正确;
如图,连接AC,交EF于G点,
∴AC⊥EF,且AC平分EF,
∵∠CAD≠∠CAF,
∴DF≠FG,
∴BE+DF≠EF,
∴③说法错误;
∵EF=2,
∴CE=CF=$\sqrt{2}$,
设正方形的边长为a,
在Rt△ADF中,
a2+(a-$\sqrt{2}$)2=4,
解得a=$\frac{\sqrt{6}}{2}$,
④说法错误,
∴正确的有①②.
故选B.
点评 本题主要考查正方形的性质的知识点,解答本题的关键是熟练掌握全等三角形的证明以及辅助线的正确作法,此题难度不大,但是有一点麻烦.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平分弦的直径垂直于弦 | |
| B. | 不在同一直线上的三点确定一个圆 | |
| C. | 矩形的四个顶点在同一个圆上 | |
| D. | 三角形的内心到三角形三边的距离相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{16}$ | B. | $\sqrt{6}$ | C. | $\sqrt{28}$ | D. | $\sqrt{\frac{1}{5}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 内错角相等 | |
| B. | 两直线平行,同旁内角相等 | |
| C. | 不相交的两条直线交平行线 | |
| D. | 过直线外一点有且只有一条直线与已知直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D,(推理时不需要写出每一步的理由)
如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D,(推理时不需要写出每一步的理由)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
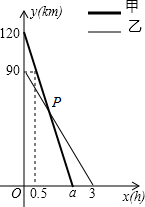 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com