
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.

(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
【答案】证明见解析
【解析】
试题(1)由OD⊥AC OD为半径,根据垂径定理,即可得![]() ,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可证得BD平分∠ABC;
,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可证得BD平分∠ABC;
(2)首先由OB=OD,易求得∠AOD的度数,又由OD⊥AC于E,可求得∠A的度数,然后由AB是⊙O的直径,根据圆周角定理,可得∠ACB=90°,继而可证得BC=OD.
试题解析:(1)∵OD⊥AC OD为半径,∴![]() ,∴∠CBD=∠ABD,
,∴∠CBD=∠ABD,
∴BD平分∠ABC;
(2)∵OB=OD,∴∠OBD=∠0DB=30°,∴∠AOD=∠OBD+∠ODB=30°+30°=60°,
又∵OD⊥AC于E,∴∠OEA=90°,
∴∠A=180°﹣∠OEA﹣∠AOD=180°﹣90°﹣60°=30°,
又∵AB为⊙O的直径,∴∠ACB=90°,在Rt△ACB中,BC=![]() AB,
AB,
∵OD=![]() AB,
AB,
∴BC=OD.


科目:初中数学 来源: 题型:
【题目】某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的![]() 时,已抢修道路 米;
时,已抢修道路 米;
(2)求原计划每小时抢修道路多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与抛物线C2互相依存.
(1)已知抛物线①:y=﹣2x2+4x+3与抛物线②:y=2x2+4x﹣1,请判断抛物线①与抛物线②是否互相依存,并说明理由.
(2)将抛物线C1:y=﹣2x2+4x+3沿x轴翻折,再向右平移m(m>0)个单位,得到抛物线C2,若抛物线C1与C2互相依存,求m的值.
(3)试问:如果对称轴不同的两条抛物线(二次函数图象)互相依存,那么它们的函数表达式中的二次项系数之间有什么数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
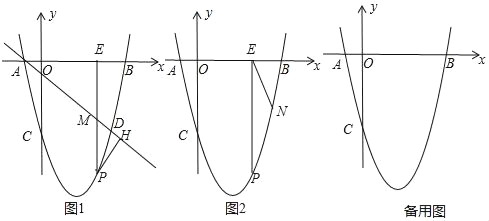
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠OAC=4.
(1)求抛物线的解析式;
(2)若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值.
(3)在(2)的条件下,如图2,在直线EP的右侧、x轴下方的抛物线上是否存在点N,过点N作NG⊥x轴交x轴于点G,使得以点E、N、G为顶点的三角形与△AOC相似?如果存在,请直接写出点G的坐标:如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
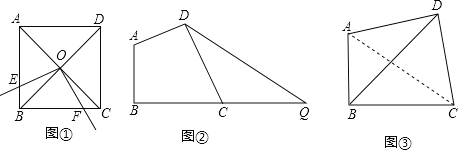
(1)如图①,正方形ABCD的边长为4,对角线AC、BD相交于点O,E是AB上点(点E不与A、B重合),将射线OE绕点O逆时针旋转90°,所得射线与BC交于点F,则四边形OEBF的面积为 .
问题探究:
(2)如图②,线段BQ=10,C为BQ上点,在BQ上方作四边形ABCD,使∠ABC=∠ADC=90°,且AD=CD,连接DQ,求DQ的最小值;
问题解决:
(3)“绿水青山就是金山银山”,某市在生态治理活动中新建了一处南山植物园,图③为南山植物园花卉展示区的部分平面示意图,在四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,AC=600米.其中AB、BD、BC为观赏小路,设计人员考虑到为分散人流和便观赏,提出三条小路的长度和要取得最大,试求AB+BD+BC的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=50°,BD,CE是∠ABC,∠ACB的平分线,则∠BOC的度数为( )
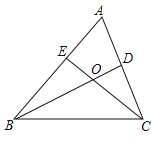
A.105°B.115°C.125°D.135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末去公园玩,发现公园一角有一种“守株待兔”的游戏,该游戏老板说明游戏规则如下:提供一只兔子和一个有A、B、C、D、E五个出口的兔笼,而且笼内的兔子从每个出口走出兔笼的机会是均等的,玩家只能将兔子从A、B两个出入口放兔子,如果兔子进笼子后从开始进入的入口出来,则玩家可获得价值5元的小兔玩具一只,否则,应付3元的参与费用.
(1)用作表或树状图列出小美参与游戏的所有可能结果,并求出小美得到玩具兔子的概率.
(2)假设有100人玩这个游戏,估计老板约赚多少钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
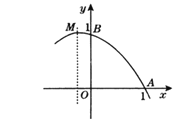
【题目】二次函数y=ax2+bx+c图象的一部分如图所示.已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,l).若此二次函数的图象与x轴的另一个交点为C.
(1)试求a,b所满足的关系式;
(2)当△AMC的面积为△ABC面积的![]() 倍时,求a的值;
倍时,求a的值;
(3)是否存在实数a,使得△ABC为直角三角形.若存在,请求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() 的对角线
的对角线![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
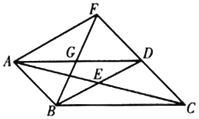
(1)求证:![]() ;
;
(2)当![]() ,
,![]() 时,请判断四边形
时,请判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
(3)当四边形![]() 是正方形时,请判断
是正方形时,请判断![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com