
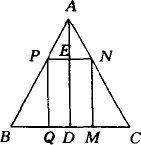
如图所示,在生产中,为了节约原材料,加工零件时常用一些边角余料,△ABC为锐角三角形废料.其中BC=12 cm,BC边上高AD=8 cm,在△ABC上截取矩形PQMN,与BC边重合,画出草图说明P,N两点落在什么位置上,才能使它的面积最大?最大面积是多少?并求出这时矩形的长和宽.
解析:
[答案]如图,设PN交AD于E.PQ长为x(cm),PN长为y cm.矩形的面积为S(cm2).则AE=(8-x)cm, ∵PN∥BC.∴∠APN=∠ABC. 又∠PAN=∠BAC,∴△APN∽△ABC.∴ 即 ∴S=PN·PQ=xy= 即S=- ∴当x=4时,S有最大值24,此时y= 此时 故当P,Q分别为AB,BD的中点时,才可使矩形PQMN的面积最大,最大面积为24cm2,此时矩形的长为6cm,宽为4cm. |


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源:新教材新学案数学九年级上册 题型:013
在日常生活和生产中,我们经常碰到一些美丽的图案,如图所示,现有两个基本图形(a)和(b),要得到这个美丽图案可用基本图形________而成


A.平移
B.旋转
C.平移和旋转均可
D.不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com