
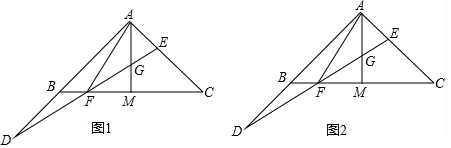
分析 (1)先用三角函数得出FN=5,BF,AM,进而用相似三角形的性质求出BD=15,即可得出AE=10,再用平行线分线段成比例定理得出MH,EH,进而用勾股定理得出EF,最后用平行线分线段成比例即可得出EG,
(2)①先构造出△BDF≌△HEF,进而判断出点H和点M重合,即可得出结论;
②先用勾股定理建立方程求出FM,AM,再用三角函数得出FN,BN,即可得出tan∠BAF=$\frac{\sqrt{5}}{7}$,最后同(1)的方法得出EG.
解答 解:(1)如图,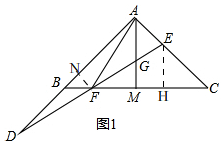 过点F作FN⊥AB,设FN=x,
过点F作FN⊥AB,设FN=x,
∵tan∠BAF=$\frac{FN}{AN}$=$\frac{1}{4}$,
∴AN=4x,
在Rt△ABC中,AB=AC,
∴∠ABC=45°,
∴BC=$\sqrt{2}$AB=25$\sqrt{2}$,BN=FN=x,BF=$\sqrt{2}$x,
∴AB=AN+BN=4x+x=25,
∴x=5,
∴BN=5,BF=5$\sqrt{2}$,
∵AM⊥BC,
∴AM=BM=CM=$\frac{1}{2}$BC=$\frac{25\sqrt{2}}{2}$,
∴FM=BM-BF=$\frac{15\sqrt{2}}{2}$,
设BD=a,
∴AE=AC-CE=25-a,AD=25+a,DN=a+5,
∵FN∥AF,
∴△DFN∽△DAE,
∴$\frac{DN}{DA}=\frac{FN}{AE}$,
∴$\frac{a+5}{25+a}=\frac{5}{25-a}$,
∴a=15,
∴BD=CE=15,AE=10,
过点E作EH⊥BC,
∵AM⊥BC,
∴EH∥AM,
∴$\frac{CH}{MH}=\frac{CE}{AE}=\frac{15}{10}=\frac{3}{2}$,
∵CH+MH=CM=$\frac{25\sqrt{2}}{2}$=AM,
∴MH=5$\sqrt{2}$,
∵EH∥AM,
∴$\frac{EH}{AM}=\frac{CE}{AC}=\frac{15}{25}=\frac{3}{5}$,
∴EH=$\frac{3}{5}$AM=$\frac{15\sqrt{2}}{2}$
∵FH=FM+MH=$\frac{25\sqrt{2}}{2}$,
根据勾股定理得,EF=$\sqrt{F{H}^{2}+E{H}^{2}}$=5$\sqrt{17}$,
∵EH∥AM,
∴$\frac{EG}{EF}=\frac{MH}{FH}$,
∴$\frac{EG}{5\sqrt{17}}=\frac{5\sqrt{2}}{\frac{25\sqrt{2}}{2}}$,
∴EG=2$\sqrt{17}$;
(2)①如图2,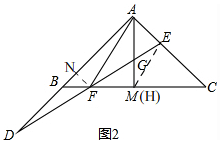 过点E作EH∥AB,
过点E作EH∥AB,
∴∠DBF=∠EHF,EH=EC,
∵EC=BD,
∴EH=BD,
在△BDF和△HEF中,$\left\{\begin{array}{l}{∠BFD=∠HFE}\\{∠DBF=∠EHF}\\{BD=EH}\end{array}\right.$,
∴△BDF≌△HEF,
∴BF=HF,
∵F是BM的中点,
∴BF=FM,
∴点H和点M重合,
∵BM=CM,
∵EM∥AB,
∴AE=CE,
即:点E是AC中点;
②过点F作FN⊥AB,
在Rt△ABM中,AM2=AB2-BM2=AB2-4FM2=9-4FM2,①
在Rt△AFM中,AM2=AF2-FM2=6-FM2,②
联立①②得,FM=1,AM=$\sqrt{5}$,
在Rt△ABM中,sin∠ABC=$\frac{AM}{AB}=\frac{\sqrt{5}}{3}$=$\frac{FN}{BF}=FN$,
∴BN=$\frac{2}{3}$,
∴AN=AB-BN=$\frac{7}{3}$,
∴tan∠BAF=$\frac{FN}{AN}$=$\frac{\frac{\sqrt{5}}{3}}{\frac{7}{3}}$=$\frac{\sqrt{5}}{7}$,
同(1)的方法得出,EG=$\frac{\sqrt{21}}{4}$.
点评 此题是三角形综合题,主要考查了锐角三角函数,直角三角形的性质,全等三角形的判定和性质,平行线分线段成比例定理,相似三角形的性质,构造全等三角形是解本题的关键,是一道计算量比较大的中考常考题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省七年级3月月考数学试卷(解析版) 题型:单选题
如下图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,
④∠B=∠DCE,其中能判定AB∥CD的条件有( )
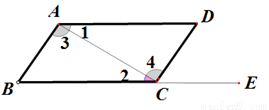
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+$\sqrt{3}$与x轴交于A(-1,0),B(3,0)两点与y轴交于点C.
如图,抛物线y=ax2+bx+$\sqrt{3}$与x轴交于A(-1,0),B(3,0)两点与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
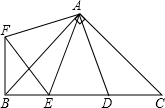 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省七年级3月月考数学试卷(解析版) 题型:单选题
如图,不能判定AB∥CD的是( )
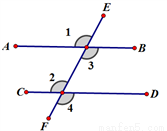
A. ∠2=∠3 B. ∠1=∠4 C. ∠1=∠2 D. ∠1=∠3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com