
 已知:如图,AC⊥BC,CD⊥CE,AC=BC,CD=CE,F为BD的中点,求证:AE=2CF,AE⊥CF.
已知:如图,AC⊥BC,CD⊥CE,AC=BC,CD=CE,F为BD的中点,求证:AE=2CF,AE⊥CF. 分析 延长CF到H使得FH=CF,AE与BC交于点O,AE与CF交于点G,首先证明△HFD≌△CFB,推出DH=BC,∠H=∠HCB,DH∥BC,再证明△ACE≌△HDC,推出AE=CH=2CF,再证明∠OGC=90°,即可解决问题.
解答 证明:延长CF到H使得FH=CF,AE与BC交于点O,AE与CF交于点G.
在△HFD和△CFB中,
$\left\{\begin{array}{l}{DF=BF}\\{∠HFD=∠BFC}\\{HF=FC}\end{array}\right.$,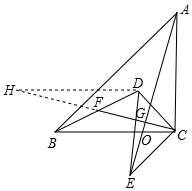
∴△HFD≌△CFB,
∴∠H=∠BCF,DH=BC=AC,
∴DH∥CB,
∴∠HDC+∠DCB=180°,
∵∠ACB=∠DCE=90°,
∴∠ACB+∠DCB=180°,
∴∠ACB+∠DCB+∠BCE=180°,
∴∠ACE+∠BCD=180°,
∴∠HDC=∠ACE,
在△ACE和△HDC中,
$\left\{\begin{array}{l}{AC=DH}\\{∠ACE=∠HDC}\\{CE=DC}\end{array}\right.$,
∴△ACE≌△HDC,
∴AE=HC=2CF,∠H=∠EAC=∠HCB,
∵∠EAC+∠AOC=90°,
∴∠HCB+∠AOC=90°,
∴∠OGC=90°,
∴AE⊥CF.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,寻找全等三角形的条件是本题的难点,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
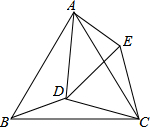 如图,△ABC和△EDC都是等边三角形,AD=$\sqrt{7}$,BD=$\sqrt{3}$,CD=2,求:
如图,△ABC和△EDC都是等边三角形,AD=$\sqrt{7}$,BD=$\sqrt{3}$,CD=2,求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
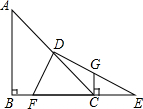 如图,△ABC中,AB=BC=a(a为常数),∠B=90°,D是AC的中点,E是BC延长线上一点,F是BC边上一点,DE⊥DF,过点C作CG⊥BE交DE于点G,则四边形DFCG的面积为$\frac{1}{4}$a2(用含a的代数式表示)
如图,△ABC中,AB=BC=a(a为常数),∠B=90°,D是AC的中点,E是BC延长线上一点,F是BC边上一点,DE⊥DF,过点C作CG⊥BE交DE于点G,则四边形DFCG的面积为$\frac{1}{4}$a2(用含a的代数式表示)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
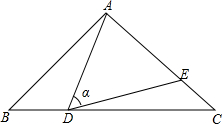 如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=α,DE交AC于点E.下列结论:
如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上(不与B,C重合)一动点,∠ADE=∠B=α,DE交AC于点E.下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
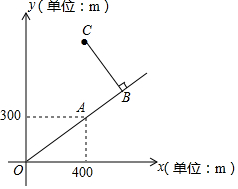 如图是根据某公园的平面示意图建立的平面直角坐标,公园的入口位于坐标原点,古塔位于点A(400,300).从古塔出发沿线OA方向前进300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C坐标是( )
如图是根据某公园的平面示意图建立的平面直角坐标,公园的入口位于坐标原点,古塔位于点A(400,300).从古塔出发沿线OA方向前进300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C坐标是( )| A. | (300,800) | B. | (400,500) | C. | (300,500) | D. | (400,800) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com