
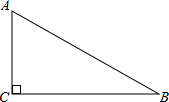
 如图,在△ABC中,∠C=90°,∠B=30°.
如图,在△ABC中,∠C=90°,∠B=30°.| 3 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
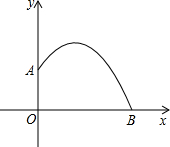 北京时间5月18日-25日,2014年世界羽联汤姆斯杯尤伯杯决赛在印度首都新德里进行,在比赛中,某次羽毛球的运动路线可以看作是抛物线y=-
北京时间5月18日-25日,2014年世界羽联汤姆斯杯尤伯杯决赛在印度首都新德里进行,在比赛中,某次羽毛球的运动路线可以看作是抛物线y=-| 1 |
| 4 |
| 3 |
| 4 |
| A、出球点A离地面点O的距离是1m | ||
| B、该羽毛球横向飞出的最远距离是3m | ||
C、此次羽毛球最高可达到
| ||
D、当羽毛球横向飞出
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com