
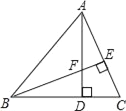
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F.
(1)求证:△ADC≌△BDF;
(2)求证:BF=2AE.
【答案】(1)见解析;(2)见解析
【解析】
(1)先判定出△ABD是等腰直角三角形,根据等腰直角三角形的性质可得AD=BD,再根据同角的余角相等求出∠CAD=∠CBE,然后利用“角边角”证明△ADC和△BDF全等;(2)根据全等三角形对应边相等可得BF=AC,再根据等腰三角形三线合一的性质可得AC=2AE,从而得证.
证明:(1)∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,AD⊥BC,
∴∠CAD+∠ACD=90°,
∠CBE+∠ACD=90°,
∴∠CAD=∠CBE,
在△ADC和△BDF中,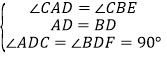 ,
,
∴△ADC≌△BDF(ASA);
(2)∵△ADC≌△BDF,
∴BF=AC,
∵AB=BC,BE⊥AC,
∴AC=2AE,
∴BF=2AE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
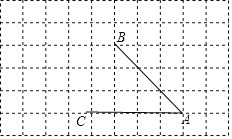
【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线;
(2)过点B画AC的垂线,垂足为点G;过点B画AB的垂线,交AC的延长线于H.
(3)点B到AC的距离是线段 的长度,线段AB的长度是点 到直线 的距离.
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1,
①b2>4ac;②4a﹣2b+c<0;③不等式ax2+bx+c>0的解集是x>3;④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2 .
上述判断中,正确的是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到对应点C,D,连接AC,BD.
(1)求出点C,D的坐标;
(2)设y轴上一点P(0,m),m为整数,使关于x,y的二元一次方程组![]() 有正整数解,求点P的坐标;
有正整数解,求点P的坐标;
(3)在(2)的条件下,若Q点在线段CD上,横坐标为n,△PBQ的面积S△PBQ的值不小于0.6且不大于4,求n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年北京奥运会后,同学们参与体育锻炼的热情高涨.为了解他们平均每周的锻炼时间,小明同学在校内随机调查了50名同学,统计并制作了如下的频数分布表和扇形统计图.根据上述信息解答下列问题: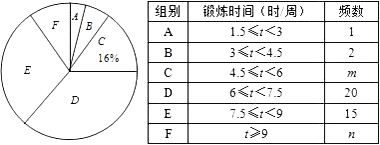
(1)m= , n=;
(2)在扇形统计图中,D组所占圆心角的度数为度;
(3)全校共有3000名学生,估计该校平均每周体育锻炼时间不少于6小时的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.
求证:AF平分∠BAC.

【答案】证明见解析.
【解析】试题分析:先根据AB=AC,可得∠ABC=∠ACB,再由垂直,可得90°的角,在△BCE和△BCD中,利用内角和为180°,可分别求∠BCE和∠DBC,利用等量减等量差相等,可得FB=FC,再易证△ABF≌△ACF,从而证出AF平分∠BAC.
试题解析:证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高,
∴BD⊥AC,CE⊥AB(高的定义).
∴∠CEB=∠BDC=90°.
∴∠ECB=90°∠ABC,∠DBC=90°∠ACB.
∴∠ECB=∠DBC(等量代换).
∴FB=FC(等角对等边),
在△ABF和△ACF中,
 ,
,
∴△ABF≌△ACF(SSS),
∴∠BAF=∠CAF(全等三角形对应角相等),
∴AF平分∠BAC.
【题型】解答题
【结束】
23
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.

(1)求证:CD=BE;
(2)已知CD=2,求AC的长;
(3)求证:AB=AC+CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com