练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．已知，在等腰三角形ABC中，三边长分别为a，b，c，其中a=6，若关于x的方程x2+（c+2）x+6-c=0有两个相等的实数根，求△ABC的周长．

    分析 由关于x的方程x2+（c+2）x+6-c=0有两个相等的实数根可求出c值，根据等腰三角形的性质结合三角形的三边关系可确定b值，再代入三角形的周长公式即可得出结论．

    解答 解：∵关于x的方程x2+（c+2）x+6-c=0有两个相等的实数根，
    ∴△=（c+2）2-4（6-c）=c2+8c-20=0，
    解得：c=2或c=-10（不合题意，舍去）．
    ∵△ABC为等腰三角形，且三边长分别为a，b，c，a=6，
    ∴a=6，b=6，c=2或a=6，b=2，c=2．
    当b=c=2时，2+2=4＜6，
    ∴2、2、6不能组成三角形，舍去．
    ∴C△ABC=a+b+c=6+6+2=14．
    答：△ABC的周长为14．

    点评 本题考查了根的判别式、三角形三边关系以及等腰三角形的性质，根据等腰三角形的性质结合三角形的三边关系确定b值是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．若反比例函数的图象过（1，-4），那么这个反比例函数的解析式为y=-$\frac{4}{x}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

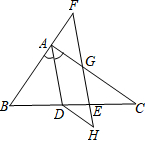    7．如图，AD平分∠BAC，点F在BA的延长线上，点E在线段CD上，EF与AC相交于点G，且∠BDA=180°-∠CEG．
    问：（1）AD与EF平行吗？请说明理由；
    （2）若点H在FE的延长线上，且∠EDH=∠C，则∠F与∠H相等吗，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．先化简，再求值$\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-{y}^{2}}$÷（$\frac{1}{x}$-$\frac{1}{y}$），其中x=$\sqrt{3}$+$\sqrt{2}$，y=$\sqrt{3}$-$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知a=-5，将代数式$\frac{{|{a-3}|•\sqrt{{a^2}-a+\frac{1}{4}}}}{{{a^2}-9}}$化简后求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图，已知Rt△ABC是直角边长为l的等腰直角三角形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…依此类推．
    ①第4个等腰直角三角形的面积是4；
    ②第n个（n＞2）等腰直角三角形的面积是2n-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．已知a，b，c为三角形的三边，化简|a+c-b|-|a-b-c|的值为（　　）
    A．0B．2aC．2（b-c）D．2（a-b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．根据下列各组a，b的值，求下列代数式的值：
    （1）当a=-$\frac{1}{2}$，b=2时，求（a+b）2-（a-b）2的值；    
    （2）当a=3，b=-2，c=-1时，求b2-4ac的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算：27x3y4z5÷（-3xyz2）•（$\frac{1}{3}$xz）2．

    查看答案和解析>>

    同步练习册答案