
【题目】如图所示,以![]() 的斜边
的斜边![]() 为边,在
为边,在![]() 的同侧作正方形
的同侧作正方形![]() ,
,![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,则
,则![]() ________.
________.

【答案】![]()
【解析】
在AC上截取CG=AB=4,连接OG,根据三角形内角和定理推出∠ABO=∠ACO,进而证出△BAO≌△CGO,推出OA=OG=![]() ,∠AOB=∠COG,得出△AOG是等腰直角三角形,再结合勾股定理计算即可得出答案.
,∠AOB=∠COG,得出△AOG是等腰直角三角形,再结合勾股定理计算即可得出答案.
在AC上截取CG=AB=4,连接OG
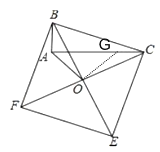
∵四边形BCEF是正方形,∠BAC=90°
∴OB=OC,∠BAC=∠BOC=90°
∴∠ABO=∠ACO
∵BA=CG,∠ABO=∠ACO,OB=OC
∴△BAO≌△CGO
∴OA=OG=![]() ,∠AOB=∠COG
,∠AOB=∠COG
∵∠BOC=∠COG+∠BOG=90°
∴∠AOG=∠AOB+∠BOG=90°,即△AOG是等腰直角三角形
∴![]() ,
,
∴AC=AG+CG=12,
∴![]() ,
,
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知点E、F分别是四边形ABCD的边AD、BC的中点,G、H分别是对角线BD、AC的中点,要使四边形EGFH是菱形,则四边形ABCD需满足的条件是( )

A.AB=CDB.AC=BDC.AC⊥BDD.AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在长方形ABCD中,AB=12cm,BC=10cm,点P从A出发,沿A→B→C→D的路线运动,到D停止;点Q从D点出发,沿D→C→B→A路线运动,到A点停止.若P、Q两点同时出发,速度分别为每秒lcm、2cm,a秒时P、Q两点同时改变速度,分别变为每秒2cm、![]() cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
(1)求出a值;
(2)设点P已行的路程为y1(cm),点Q还剩的路程为y2(cm),请分别求出改变速度后,y1、y2和运动时间x(秒)的关系式;
(3)求P、Q两点都在BC边上,x为何值时P、Q两点相距3cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.
(1)求打包成件的帐篷和食品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料一:小明计算![]() ,发现其结果为
,发现其结果为![]() 计算
计算![]() ,发现其结果为
,发现其结果为![]()
阅读材料二:小华发现一个有趣的算式![]()
(1)请模仿小华的算式,再写出一个类似的正确算式;
(2)请用字母表示小华算式的规律;
(3)请用阅读材料一中蕴含的数学规律或你掌握的数学知识说明(2)中的规律为何成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
①试说明BE·AD=CD·AE;
②根据图形特点,猜想![]() 可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)
可能等于哪两条线段的比?并证明你的猜想,(只须写出有线段的一组即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为 ( ) .

A.4.8B.3![]() C.5D.3
C.5D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD和△ACE中,AB=AD,AC=AE,∠BAD=∠CAE,连接BC、DE相交于点F,BC与AD相交于点G.

(1)试判断线段BC、DE的数量关系,并说明理由;
(2)若BC平分∠ABD,求证线段FD是线段FG 和 FB的比例中项.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com