
����Ŀ����ͼ����֪�ڡ�ABC�У�AB��AC��BC��12���ף���DΪAB��һ����BD��8���ף���P���߶�BC����2����/����ٶ���B����C���˶������˶�ʱ��Ϊt��ͬʱ����Q���߶�CA����C����A���˶�.

��1���ú�t��ʽ�ӱ�ʾPC�ij�Ϊ_______________;
��2������Q���˶��ٶ����p���˶��ٶ���ȣ���t��2ʱ��������BPD��������CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
��3������Q���˶��ٶ����P���˶��ٶȲ���ȣ��������Q���˶��ٶ��Ƕ���ʱ���ܹ�ʹ������BPD��������CQPȫ��?
���𰸡�(1)PC=12-2t��(2)��BPD����CQP���ɼ���⣻(3) ![]() cm/s
cm/s
��������
(1)����BC=12cm����P���߶�BC����2����/����ٶ���B����C���˶������Ե�t��ʱ���˶�2t�����PC=12-2t.��2������Q���˶��ٶ����p���˶��ٶ���ȣ���t��2sʱ����CQ=4cm��BP=4cm����ΪBC=12cm������PC=8cm,����ΪBD=8cm��AB=AC�����ԡ�B=��C,��������BPD�զ�CQP.(3) ��֪��B=��C��BP��CQ�����ݦ�BPD�զ�CQP�ó� BP=PC���������ʱ��t�������v����.
(1)�������PC=12-2t
��2������Q���˶��ٶ����p���˶��ٶ���ȣ���t��2sʱ����CQ=4cm��BP=4cm���� BC=12cm����PC=8cm,�֡�BD=8cm��AB=AC�����B=��C���ڦ�BPD�ͦ�CQP�У�CQ=BP, ��B=��C,PC=BD���তBPD�զ�CQP��SAS��.
(3)����Q���˶��ٶ����P���˶��ٶȲ���ȣ���Vp��VQ,��BP��CQ,�֡ߡ�BPD�ա�CPQ,��B=��C,��BP=PC=6cm,CQ=BD=8cm,���P����Q�˶���ʱ�� t= ![]() =3s ,
=3s ,
��VQ =![]() =
=![]() =
=![]() cm/s����Q���ٶ�Ϊ
cm/s����Q���ٶ�Ϊ![]() cm/s.
cm/s.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�DΪBC����һ�㣮
(1)��ͼ�٣���Rt��ABC�У���C��90�㣬����ABC����AD�۵�����C����AB���ϣ�����ֱ�ߺ�Բ��������D����д������������ͼ�ۼ�����
(2)��ͼ��������ABC���Ź���D��ֱ���۵�����C����AB���ϵ�E����
����DE��AB������ΪE������ֱ�ߺ�Բ��������D����д������������ͼ�ۼ�����
����AB��![]() ��BC��3����B��45�㣬��CD��ȡֵ��Χ��
��BC��3����B��45�㣬��CD��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ�����װ��10���������������ͬ��С��ÿ��С��ĺ���ֱ���1��2��3��4��5��6��7��8��9��10�����dz��ҡ�ȣ���������������һ��С�涨����С������ܱ�3����ʱ����ʤ������С������ܱ�5����ʱ���һ�ʤ�������Ϸ�Լ���˫����ƽô����˵�����ɣ��������ƽ��Ӧ���������Ϸ������ܶ�˫����ƽ������Ϸ��˫����ƽ��ԭ���ǣ�˫����ʤ�ĸ�����ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c(a��0)��ͼ����x�ύ��A��B���㣬��y�ύ��C�㣬�ҶԳ���Ϊֱ��x=1����B����Ϊ(��1��0)����������ĸ����ۣ���2a+b=0����4a��2b+c��0����ac��0���ܵ�y��0ʱ��x����1��x��3��������ȷ�ĸ����ǣ� ��

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У�AB=AC=8��BO=![]() AB����MΪBC����һ���㣬���߶�OM�Ƶ�O����ʱ�뷽����ת90����ON������AN��CN�����CAN�ܳ�����СֵΪ________.
AB����MΪBC����һ���㣬���߶�OM�Ƶ�O����ʱ�뷽����ת90����ON������AN��CN�����CAN�ܳ�����СֵΪ________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������120���������ˣ�ÿ������ÿ���������˨25������ĸ20�������һ����˨��������ĸ���һ�� ����ôÿ�찲�Ŷ�������������˨������������������ĸ������ʹÿ�����������IJ�Ʒ�������ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˿����������赸����ֽ�������γ�������ѧ�������������������ȡ�˲���ѧ��������������Ȥ��������˵��飨ÿ�˴���ֻ��ѡһ����������������Ƴ���ͼ����ͳ��ͼ��������ͼ����Ϣ������⣮
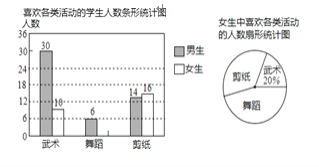
��1��������ͳ��ͼ����������
��2���������������������� ��
��3����֪��У��1200��ѧ�������������������ȫУѧ����ϲ����ֽ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD��OEƽ�֡�BOC��OF��OE��OP��CD����ABO��40�㣬�����н��ۣ�����BOE��70�㣻��OFƽ�֡�BOD������POE����BOF������POB��2��DOF��������ȷ������_____����ţ�
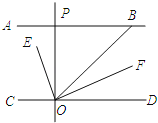
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��̣�m��1��x2��x��2=0��
��1����x=��1�Ƿ��̵�һ��������m��ֵ�ͷ��̵���һ����
��2����mΪ��ʵ��ʱ��������ʵ������
��3����x1��x2�Ƿ��̵�����������![]() ������ʵ��m��ֵ��
������ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com