练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

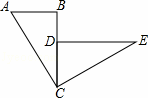
    如图，已知：BC与CD重合，∠ABC=∠CDE=90°，△ABC≌△CDE，并且△CDE可由△ABC逆时针旋转而得到．请你利用尺规作出旋转中心O（保留作图痕迹，不写作法，注意最后用墨水笔加黑），并直接写出旋转角度是　　．


    90°解：如图所示：旋转角度是90°．

    故答案为：90°．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    若，则化简后为                                            【   】

    A       B.    C.     D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    x1，x2是关于x的一元二次方程x2﹣mx+m﹣2=0的两个实数根，是否存在实数m使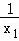+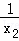=0成立？则正确的是结论是（　　）

    　

    A．

    m=0时成立

    B．

    m=2时成立

    C．

    m=0或2时成立

    D．

    不存在

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，直线MN与⊙O相切于点M，ME=EF且EF∥MN，则cos∠E=　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    给定直线l：y=kx，抛物线C：y=ax2+bx+1．

    （1）当b=1时，l与C相交于A，B两点，其中A为C的顶点，B与A关于原点对称，求a的值；

    （2）若把直线l向上平移k2+1个单位长度得到直线r，则无论非零实数k取何值，直线r与抛物线C都只有一个交点．

    ①求此抛物线的解析式；

    ②若P是此抛物线上任一点，过P作PQ∥y轴且与直线y=2交于Q点，O为原点．求证：OP=PQ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：_______

    查看答案和解析>>

    科目：初中数学 来源： 题型：


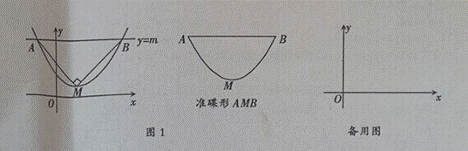
    如图1，抛物线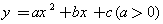的顶点为M，直线y=m与x轴平行，且与抛物线交于点A，B，若三角形AMB为等腰直角三角形，我们把抛物线上A、B两点之间的部分与线段AB围成的图形称为该抛物线对应的准蝶形，线段AB称为碟宽，顶点M称为碟顶，点M到线段AB的距离称为碟高。

    （1）       抛物线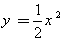对应的碟宽为________;抛物线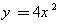对应的碟宽为______;抛物线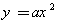（a>0）对应的碟宽为________;抛物线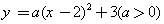对应的碟宽_____;

    （2）       若抛物线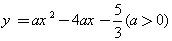对应的碟宽为6，且在x轴上，求a的值；

    （3）       将抛物线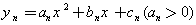的对应准蝶形记为Fn（n=1,2,3，…），定义F1，F2，…..Fn为相似准蝶形，相应的碟宽之比即为相似比。若Fn与Fn-1的相似比为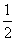，且Fn的碟顶是Fn-1的碟宽的中点，现在将（2）中求得的抛物线记为y1，其对应的准蝶形记为F1.

    ①     求抛物线y2的表达式

    ② 若F1的碟高为h1,F2的碟高为h2，…Fn的碟高为hn,则hn=_______,Fn的碟宽右端点横坐标为_______;F1，F2，…..Fn的碟宽右端点是否在一条直线上？若是，直接写出改直线的表达式；若不是，请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在□ABCD中，以点A为圆心，AB的长为半径的圆恰好与CD相切于点C，交AD于点E，延长BA与⊙A相交于点F．若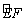的长为，则图中阴影部分的面积为    ．

    查看答案和解析>>

    同步练习册答案