
【题目】如图,一次函数y=kx+3的图象与反比例函数![]() 的图象交于P、Q两点,PA⊥x轴于点A,一次函数的图象分别交x轴、y轴于点C、点B,其中OA=6,且
的图象交于P、Q两点,PA⊥x轴于点A,一次函数的图象分别交x轴、y轴于点C、点B,其中OA=6,且![]() .
.
(1)求一次函数和反比例函数的表达式;
(2)求△APQ的面积;
(3)根据图象写出当x取何值时,一次函数的值小于反比例函数的值.

【答案】(1)y=-![]() x+3,y=-
x+3,y=-![]() ;(2)S△APQ=30;(3)当-4<x<0或x>6时,一次函数的值小于反比例函数的值.
;(2)S△APQ=30;(3)当-4<x<0或x>6时,一次函数的值小于反比例函数的值.
【解析】
(1)根据题意求得C(2,0).将C代入y=kx+3中,即可得到一次函数的表达式.
根据题意求得P(6,-6).将点P(6,-6)代入反比例函数y=![]() ,即可得到反比例函数的表达式.
,即可得到反比例函数的表达式.
(2)联立直线PQ与反比例函数解析式,得到Q点坐标.再根据三角形的面积公式即可得到答案.
(3)通过观察图像即可得到答案.
(1)∵OA=6,且![]() ,
,
∴OA=3OC=6,
∴OC=2,即C(2,0).
将C(2,0)代入y=kx+3中,
得:0=2k+3,解得:k=-![]() ,
,
∴一次函数的表达式为y=-![]() x+3.
x+3.
令y=-![]() x+3中x=6,则y=-6,
x+3中x=6,则y=-6,
∴P(6,-6).
∵点P(6,-6)在反比例函数y=![]() 的图象上,
的图象上,
∴m=6×(-6)=-36,
∴反比例函数的表达式为y=-![]() .
.
(2)联立直线PQ与反比例函数解析式,
得: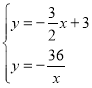 ,解得:
,解得:![]() ,或
,或![]() ,
,
∴Q(-4,9).
∴S△APQ=![]() AC(yQ-yP)=
AC(yQ-yP)=![]() ×(6-2)×[9-(-6)]=30.
×(6-2)×[9-(-6)]=30.
(3)观察函数图象发现:
当-4<x<0或x>6时,一次函数图象在反比例函数图象的下方,
∴当-4<x<0或x>6时,一次函数的值小于反比例函数的值.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
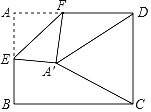
【题目】如图,在矩形纸片ABCD中,AB=4,BC=4![]() ,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店专售一款电动牙刷,其成本为20元/支,销售中发现,该商品每天的销售量y(支)与销售单价x(元/支)之间存在如图所示的关系.
(1)求y与x之间的函数关系式.
(2)由于湖北省武汉市爆发了新型冠状病毒肺炎(简称“新冠肺炎”)疫情,该网店店主决定从每天获得的利润中抽出200元捐献给武汉,为了保证捐款后每天剩余利润不低于550元,如何确定这款电动牙刷的销售单价?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法正确的是( )
A.小明做了![]() 次掷图钉的实验,发现
次掷图钉的实验,发现![]() 次钉尖朝上,由此他说钉尖朝上的概率是
次钉尖朝上,由此他说钉尖朝上的概率是![]()
B.一组对边平行,另一组对边相等的四边形是平行四边形
C.点![]() 都在反比例函数
都在反比例函数![]() 图象上,且
图象上,且![]() 则
则![]() ;
;
D.对于一元二元方程![]() ,若
,若![]() 则方程的两个根互为相反数
则方程的两个根互为相反数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳某百果园店售卖赣南脐橙,已知每千克脐橙的成本价为![]() 元,在销售脐橙的这
元,在销售脐橙的这![]() 天时间内,销售单价
天时间内,销售单价![]() (元/千克)与时间第
(元/千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数),日销售量
为整数),日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数)
为整数)
(1)请你直接写出日销售利润![]() (元)与时间第
(元)与时间第![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)该店有多少天日销售利润不低于![]() 元?
元?
(3)在实际销售中,该店决定每销售![]() 千克脐橙,就捐赠
千克脐橙,就捐赠![]() 元给希望工程,在这
元给希望工程,在这![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】揭西县围绕“推进‘六稳’,拉动消费”为主题,举办“揭西人游揭西”活动,从4月份到6月份,分批次免费游览县内相关旅游景区景点.某班级全班同学分别从A、B、C、D、E五个景区中选出自己最喜欢的一个,绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
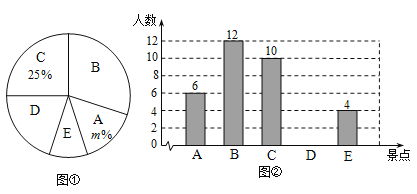
(1)图①中m的值为.扇形统计图中,B景区所对的圆心角的大小是;
(2)补全条形统计图;
(3)甲乙两个同学分别从A、B、C、D四个景区中随机挑出一个景区各自游玩,请用树状图或列表的方法求出他们刚好选到同一个景区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在完善基础设施、改善市容市貌、提升城市品质过程中,2019年我市开展人行道改造工程,需要花岗岩地板砖铺设人行道.现租用甲、乙两种货车运载地板砖,已知一辆甲车每次运载的重量比一辆乙车多2吨,且甲车运载16吨地板砖和乙车运载12吨地板砖所用的车辆数相同.
(1)甲、乙两种货车每次运载地板砖各多少吨?
(2)现租用甲车a辆、乙车b辆,刚好运载地板砖100吨,且a≤3b,共有多少种租车方案?
(3)在(2)中已知一辆甲车每次的运费是380元,一辆乙车每次的运费是300元,如何租用甲、乙两种车可使得总运费最低?求出最低总运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
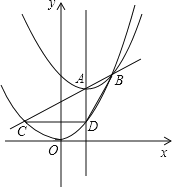
【题目】A是直线x=1上一个动点,以A为顶点的抛物线y1=a(x﹣1)2+t和抛物线y2=ax2交于点B(A,B不重合,a是常数),直线AB和抛物线y2=ax2交于点B,C,直线x=1和抛物线y2=ax2交于点D.(如图仅供参考)
(1)求点B的坐标(用含有a,t的式子表示);
(2)若a<0,且点A向上移动时,点B也向上移动,求![]() 的范围;
的范围;
(3)当B,C重合时,求![]() 的值;
的值;
(4)当a>0,且△BCD的面积恰好为3a时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com