
如图①,已知Rt△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B、C在AE的两侧,BD⊥DE,CE⊥DE,分别于D、E.
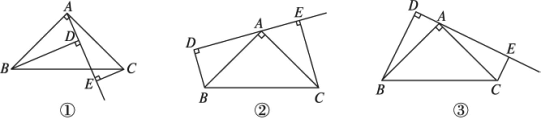
(1)判断BD与DE+CE的关系,并说明理由.
(2)若直线AE绕A点旋转到如图②(BD<CE)所示位置时,其余条件不变,则BD与DE、CE的关系如何?请说明理由.
(3)若直线AE绕A点旋转到如图③(BD>CE)所示位置时,其余条件不变,则BD与DE、CE的关系如何?请直接写出结果,不用证明.
(4)归纳(1)(2)(3),请用简洁的语言表述BD、DE、CE的关系.
|
解:(1)BD=DE+CE. 理由:∵∠BAC=90°,∠BAD+∠BAC+∠CAE=180°,∴∠BAD+∠CAE=90°. ∵BD⊥DE,∴∠BAD+∠ABD=90°. ∴∠ABD=∠CAE. 在△ABD与△CAE中, ∴△ABD≌△CAE(AAS). ∴DA=CE,AE=BD(全等三角形的对应边相等). ∵AE=DA+DE,∴BD=DE+CE. (2)BD=DE-CE,理由同上. (3)BD=DE-CE. (4)归纳(1)(2)(3)可知,结论表示为: 当B、C在AE两侧时,BD=DE+CE. 当B、C在AE同侧时,BD=DE-CE. 分析:本题反映了动态几何中的量的关系,其关键是猜想规律,再运用有关的几何知识进行证明. 三种情况下,都可以证明△ABD≌△CAE,把BD、CE转换到直线AE上,分不同的情况讨论. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图1.已知Rt△ABC,∠C=90°,∠A=30°,AB=2,M是斜边AB上的一个动点,垂足为H,以MH为对角线作菱形MPHQ,其中,顶点P始终在斜边AB上.连接PQ并延长交AC于点E,以E为圆心,EC长为半径作⊙E.
如图1.已知Rt△ABC,∠C=90°,∠A=30°,AB=2,M是斜边AB上的一个动点,垂足为H,以MH为对角线作菱形MPHQ,其中,顶点P始终在斜边AB上.连接PQ并延长交AC于点E,以E为圆心,EC长为半径作⊙E.查看答案和解析>>
科目:初中数学 来源: 题型:

| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com