
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)在图中找出一对相似三角形,并说明理由;
(2)若AB=8,AD=![]() ,AF=
,AF=![]() ,求AE的长.
,求AE的长.
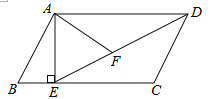
【答案】(1)△ADF∽△DEC,见解析;(2)6
【解析】
(1)根据∠AFE=∠B且四边形ABCD是平行四边形得出∠AFD=∠C,再根据平行得出∠ADF=∠DEC,从而证明△ADF∽△DEC;
(2)由(1)的相似对应边成比例计算出DE,再根据勾股定理计算AE的长度.
(1)△ADF∽△DEC
理由:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
在△ADF与△DEC中,![]() ,
,
∴△ADF∽△DEC
(2)解:∵四边形ABCD是平行四边形,
∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴![]() ,
,
∴DE=![]() .
.
在Rt△ADE中,AE=![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
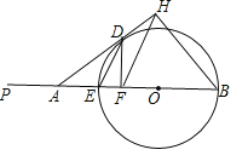
【题目】已知,如图,EB是![]() 的直径,且
的直径,且![]() ,在BE的延长线上取点P,使
,在BE的延长线上取点P,使![]() ,A是EP上一点,过A作
,A是EP上一点,过A作![]() 的切线,切点为D,过D作
的切线,切点为D,过D作![]() 于F,过B作AD的垂线BH,交AD的延长线于
于F,过B作AD的垂线BH,交AD的延长线于![]() 当点A在EP上运动,不与E重合时:
当点A在EP上运动,不与E重合时:
![]() 是否总有
是否总有![]() ,试证明你的结论;
,试证明你的结论;
![]() 设
设![]() ,
,![]() ,求y和x的函数关系,并写出x的取值范围.
,求y和x的函数关系,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
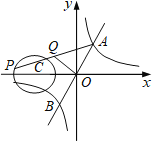
【题目】如图,一次函数y=2x与反比例函数y=![]() (k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为
(k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为![]() ,则k的值为( )
,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知,在△ABC中,∠BCA=90°,AC=kBC,点D,E分别在边BC,AC上,且AE=kCD,作线段DF⊥DE,且DE=kDF,连接EF交AB于点G.
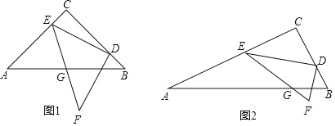
(1)如图1,当k=1时,求证:①∠CED=∠BDF,②AG=GB;
(2)如图2,当k≠1时,猜想![]() 的值,并说明理由;
的值,并说明理由;
(3)当k=2,AE=4BD时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 过点
过点![]() ,且与直线
,且与直线![]() 交于B、C两点,点B的坐标为
交于B、C两点,点B的坐标为![]() .
.
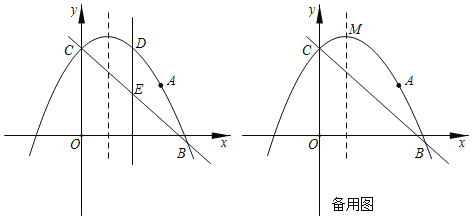
(1)求抛物线的解析式;
(2)点D为抛物线上位于直线![]() 上方的一点,过点D作
上方的一点,过点D作![]() 轴交直线
轴交直线![]() 于点E,点P为对称轴上一动点,当线段
于点E,点P为对称轴上一动点,当线段![]() 的长度最大时,求
的长度最大时,求![]() 的最小值;
的最小值;
(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使![]() ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
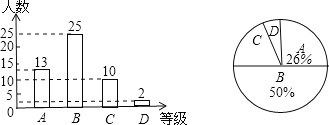
【题目】某校为了了解九年级学生体育测试成绩情况,以九年(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分﹣74分;D级:60分以下)
(1)求出D级学生的人数占全班总人数的百分比;
(2)求出扇形统计图中C级所在的扇形圆心角的度数;
(3)该班学生体育测试成绩的中位数落在哪个等级内;
(4)若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则称这个点为强点.例如,图中过点P分別作x轴,y轴的垂线与坐标轴围成矩形OAPB的周长与面积相等,则点P是强点.
(1)点M(l,2),N(4,4),Q(6,-3)中,是强点的有 ;
(2)若强点P(2a,3)在双曲线![]() 上,求a和b的值.
上,求a和b的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药店销售口罩,进价15元,售价20元,为防控新冠肺炎疫情,药店决定凡是一次性购买10个以上的客户,每多买一个,售价就降低0.1元(顾客所购买的全部口罩),但最低价是17元/个.
(1)顾客一次性至少购买多少个口罩时,才能以最低价17元/个购买?
(2)写出一次性购买x个口罩时(x>10),药店的利润y(元)与购买量x(个)之间的函数关系式;
(3)在销售过程中,药店发现一次性卖出36个口罩时比卖出26个口罩的钱少,为了使每次销售均能达到多卖就能多获利,在其他促销条件不变的情况下,最低价应确定为每个多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com