
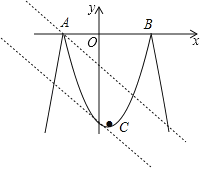
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )

A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
【答案】D
【解析】如图,解方程﹣x2+x+6=0得A(﹣2,0),B(3,0),再利用折叠的性质求出折叠部分的解析式为y=(x+2)(x﹣3),即y=x2﹣x﹣6(﹣2≤x≤3),然后求出直线y=﹣x+m经过点A(﹣2,0)时m的值和当直线y=﹣x+m与抛物线y=x2﹣x﹣6(﹣2≤x≤3)有唯一公共点时m的值,从而得到当直线y=﹣x+m与新图象有4个交点时,m的取值范围.
如图,当y=0时,﹣x2+x+6=0,解得x1=﹣2,x2=3,则A(﹣2,0),B(3,0),
将该二次函数在x轴上方的图象沿x轴翻折到x轴下方的部分图象的解析式为y=(x+2)(x﹣3),
即y=x2﹣x﹣6(﹣2≤x≤3),
当直线y=﹣x+m经过点A(﹣2,0)时,2+m=0,解得m=﹣2;
当直线y=﹣x+m与抛物线y=x2﹣x﹣6(﹣2≤x≤3)有唯一公共点时,方程x2﹣x﹣6=﹣x+m有相等的实数解,解得m=﹣6,
所以当直线y=﹣x+m与新图象有4个交点时,m的取值范围为﹣6<m<﹣2,
故选D.


科目:初中数学 来源: 题型:
【题目】随着手机的普及,微信(一种聊天软件)的兴起,许多人抓住这种机会,做起了“微商”很多农产品也改变了原来的销售模式,实行了网上销售,刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖![]() 斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负单位:斤);
斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负单位:斤);
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 斤;
(2)根据记录的数据可知该周销售量最多的一天比销售量最少的一天多销售 斤;
(3)本周实际销售总量是否达到了计划数量?试通过计算说明理由.
(4)若冬枣每斤按![]() 元出售,每斤冬枣的运费平均
元出售,每斤冬枣的运费平均![]() 元(运费由小明承担),那么小明本周一共收入多少元?
元(运费由小明承担),那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在直线于点F.
(1)当点E在线段BD上移动时,如图(1)所示,求证:BC﹣DE=![]() DF.
DF.
(2)当点E在直线BD上移动时,如图(2)、图(3)所示,线段BC、DE与DF又有怎样的数量关系?请直接写出你的猜想,不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
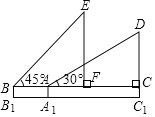
【题目】如图是小红在一次放风筝活动中某时段的示意图,她在A处时的风筝线(整个过程中风筝线近似地看作直线)与水平线构成30°角,线段AA1表示小红身高1.5米.
(1)当风筝的水平距离AC=18米时,求此时风筝线AD的长度;
(2)当她从点A跑动9![]() 米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10
米到达点B处时,风筝线与水平线构成45°角,此时风筝到达点E处,风筝的水平移动距离CF=10![]() 米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
米,这一过程中风筝线的长度保持不变,求风筝原来的高度C1D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六盘水市梅花山国际滑雪自建成以来,吸引大批滑雪爱好者,一滑雪者从山坡滑下,测得滑行距离y(单位:cm)与滑行时间x(单位:s)之间的关系可以近似的用二次函数来表示.
滑行时间x/s | 0 | 1 | 2 | 3 | … |
滑行距离y/cm | 0 | 4 | 12 | 24 | … |
(1)根据表中数据求出二次函数的表达式.现测量出滑雪者的出发点与终点的距离大约800m,他需要多少时间才能到达终点?
(2)将得到的二次函数图象补充完整后,向左平移2个单位,再向上平移5个单位,求平移后的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
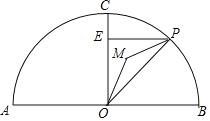
【题目】如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.
(1)求∠OMP的度数;
(2)当点P在半圆上从点B运动到点A时,求内心M所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=y1+y2,y1与x成正比例,y2与x-2成正比例,当x=1时,y=0;当x=-3时,y=4.
(1)求y与x的函数关系式,并说明此函数是什么函数;
(2)当x=3时,求y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.

(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com