
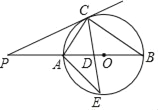
【题目】如图,AB是⊙O的直径,∠ACB的平分线交AB于点D,交⊙O于点E,过点C作⊙O的切线CP交BA的延长线于点P,连接AE.
(1)求证:PC=PD;
(2)若AC=6cm,BC=8cm,求线段AE、CE的长.
【答案】(1)详见解析;(2)EC=7![]() ,AE=
,AE=![]() .
.
【解析】
(1)如图1中,连接OC、OE.利用等角的余角相等,证明∠PCD=∠PDC即可;
(2)如图2中.作EH⊥BC于H,EF⊥CA于F.首先证明Rt△AEF≌Rt△BEH,推出AF=BH,设AF=BH=x,再证明四边形CFEH是正方形,推出CF=CH,可得6+x=8-x,推出x=1,延长即可解决问题;
(1)证明:如图1中,连接OC、OE.
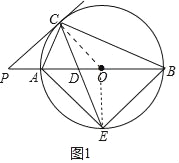
∵AB 直径,
∴∠ACB=90°,
∴CE平分∠ACB,
∴∠ECA=∠ECB=45°,
∴![]() ,
,
∴OE⊥AB,
∴∠DOE=90°,
∵PC是切线,
∴OC⊥PC,
∴∠PCO=90°,
∵OC=OE,
∴∠OCE=∠OEC,
∵∠PCD+∠OCE=90°,∠ODE+∠OEC=90°,∠PDC=∠ODE,
∴∠PCD=∠PDC,
∴PC=PD.
(2)如图2中.作EH⊥BC于H,EF⊥CA于F.
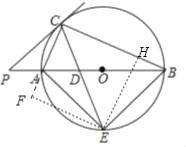
∵CE平分∠ACB,EH⊥BC于H,EF⊥CA于F,
∴EH=EF,∠EFA=∠EHB=90°,
∵![]() ,
,
∴AE=BE,
∴Rt△AEF≌Rt△BEH,
∴AF=BH,设AF=BH=x,
∵∠F=∠FCH=∠CHE=90°,
∴四边形CFEH是矩形,
∵EH=EF,
∴四边形CFEH是正方形,
∴CF=CH,
∴6+x=8﹣x,
∴x=1,
∴CF=FE=7,
∴EC=![]() CF=7
CF=7![]() ,
,
AE=![]() =
=![]() =5
=5![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,正确说法的个数有( )
①角是轴对称图形,对称轴是角的平分线;②等腰三角形至少有![]() 条对称轴,至多有
条对称轴,至多有![]() 条对称轴;③关于某直线对称的两个三角形一定是全等三角形;④两图形关于某直线对称,对称点一定在直线的两旁.
条对称轴;③关于某直线对称的两个三角形一定是全等三角形;④两图形关于某直线对称,对称点一定在直线的两旁.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
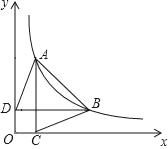
【题目】如图,已知双曲线y=![]() (x>0)图象上两点,过A、B两点分别作x轴、y轴的垂线,垂足分别为C、D,连接AD、BC,则:
(x>0)图象上两点,过A、B两点分别作x轴、y轴的垂线,垂足分别为C、D,连接AD、BC,则:
(1)若A、B两点的坐标分别是(1,4)、(4,1),求S△OAB;
(2)证明:S△ABD=S△ABC.
(3)连接CD,判断CD与AB的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富少年儿童的业余文化生活,某社区要在如图所示的AB所在的直线上建一图书阅览室,该社区有两所学校,所在的位置分别在点C和点D处。CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:阅览室E建在距A点多远时,才能使它到C、D两所学校的距离相等?
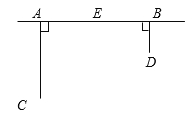
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,AF=4,CF=2,求AE的长.
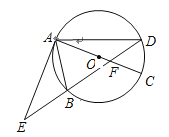
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形 ABCD 折叠,折痕交边 AB,CD 分别于点 E,F,顶点 A 落在 BC 边上的 M 点,边 AD 折叠后与边 CD 交于点 N,如果 BE=2,正方形ABCD 的周长为 20,则 CN 的长为( )
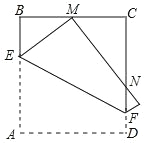
A. ![]() (
(![]() ﹣1) B. 2(
﹣1) B. 2(![]() ﹣1) C.
﹣1) C. ![]() (5
(5![]() ﹣13) D. ﹣2
﹣13) D. ﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生每天参加户外活动的情况,随机抽查了100名学生每天参加户外活动的时间情况,并将抽查结果绘制成如图所示的扇形统计图.
请你根据图中提供的信息解答下列问题:

(1)请直接写出图中![]() 的值,并求出本次抽查中学生每天参加户外活动时间的中位数;
的值,并求出本次抽查中学生每天参加户外活动时间的中位数;
(2)求本次抽查中学生每天参加户外活动的平均时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦DE交AB于点F,⊙O的切线BC与AD的延长线交于点C,连接AE.
(1)试判断∠AED与∠C的数量关系,并说明理由;
(2)若AD=3,∠C=60°,点E是半圆AB的中点,则线段AE的长为 .
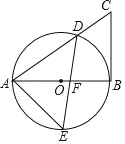
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com