
【题目】已知:△ABC是等腰直角三角形,∠BAC=90°,将△ABC绕点C顺时针方向旋转得到△A′B′C,记旋转角为α,当90°<α<180°时,作A′D⊥AC,垂足为D,A′D与B′C交于点E.
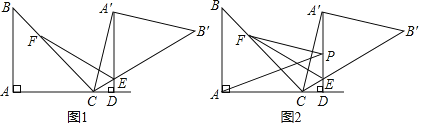
(1)如图1,当∠CA′D=15°时,作∠A′EC的平分线EF交BC于点F.
①写出旋转角α的度数;
②求证:EA′+EC=EF;
(2)如图2,在(1)的条件下,设P是直线A′D上的一个动点,连接PA,PF,若AB=![]() ,求线段PA+PF的最小值.(结果保留根号)
,求线段PA+PF的最小值.(结果保留根号)
【答案】(1)①105°,②见解析;(2)![]()
【解析】
(1)①解直角三角形求出∠A′CD即可解决问题,
②连接A′F,设EF交CA′于点O,在EF时截取EM=EC,连接CM.首先证明△CFA′是等边三角形,再证明△FCM≌△A′CE(SAS),即可解决问题.
(2)如图2中,连接A′F,PB′,AB′,作B′M⊥AC交AC的延长线于M.证明△A′EF≌△A′EB′,推出EF=EB′,推出B′,F关于A′E对称,推出PF=PB′,推出PA+PF=PA+PB′≥AB′,求出AB′即可解决问题.
①解:由∠CA′D=15°,可知∠A′CD=90°-15°=75°,所以∠A′CA=180°-75°=105°即旋转角α为105°.
②证明:连接A′F,设EF交CA′于点O.在EF时截取EM=EC,连接CM.
∵∠CED=∠A′CE+∠CA′E=45°+15°=60°,

∴∠CEA′=120°,
∵FE平分∠CEA′,
∴∠CEF=∠FEA′=60°,
∵∠FCO=180°﹣45°﹣75°=60°,
∴∠FCO=∠A′EO,∵∠FOC=∠A′OE,
∴△FOC∽△A′OE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠COE=∠FOA′,
∴△COE∽△FOA′,
∴∠FA′O=∠OEC=60°,
∴△A′CF是等边三角形,
∴CF=CA′=A′F,
∵EM=EC,∠CEM=60°,
∴△CEM是等边三角形,
∠ECM=60°,CM=CE,
∵∠FCA′=∠MCE=60°,
∴∠FCM=∠A′CE,
∴△FCM≌△A′CE(SAS),
∴FM=A′E,
∴CE+A′E=EM+FM=EF.
(2)解:如图2中,连接A′F,PB′,AB′,作B′M⊥AC交AC的延长线于M.
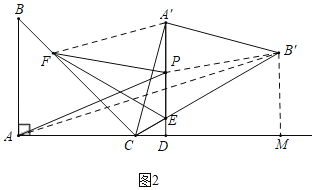
由②可知,∠EA′F=′EA′B′=75°,A′E=A′E,A′F=A′B′,
∴△A′EF≌△A′EB′,
∴EF=EB′,
∴B′,F关于A′E对称,
∴PF=PB′,
∴PA+PF=PA+PB′≥AB′,
在Rt△CB′M中,CB′=BC=![]() AB=2,∠MCB′=30°,
AB=2,∠MCB′=30°,
∴B′M=![]() CB′=1,CM=
CB′=1,CM=![]() ,
,
∴AB′=![]() =
=![]() =
=![]() .
.
∴PA+PF的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中,有三个除颜色外其它均相同的小球,其中两个黑色,一个红色.
(1)请用表格或树状图求出:一次随机取出2个小球,颜色不同的概率.
(2)如果老师在布袋中加入若干个红色小球.然后小明通过做实验的方式猜测加入的小球数,小 明每次換出一个小球记录下慎色并放回,实验数据如下表:
实验次数 | 100 | 200 | 300 | 400 | 500 | 1000 |
摸出红球 | 78 | 147 | 228 | 304 | 373 | 752 |
请你帮小明算出老师放入了多少个红色小球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解九年级学生对“八礼四仪”的掌握情况,对该年级的500名同学进行问卷测试,并随机抽取了10名同学的问卷,统计成绩如下:
得分 | 10 | 9 | 8 | 7 | 6 |
人数 | 3 | 3 | 2 | 1 | 1 |
(1)计算这10名同学这次测试的平均得分;
(2)如果得分不少于9分的定义为“优秀”,估计这 500名学生对“八礼四仪”掌握情况优秀的人数;
(3)小明所在班级共有40人,他们全部参加了这次测试,平均分为7.8分.小明的测试成绩是8分,小明说,我的测试成绩在班级中等偏上,你同意他的观点吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个不透明的袋子,甲袋子里装有标有![]() 两个数字的
两个数字的![]() 张卡片,乙袋子里装有标有
张卡片,乙袋子里装有标有![]() 三个数字的
三个数字的![]() 张卡片,两个袋子里的卡片除标有的数字不同外,其大小质地完全相同.
张卡片,两个袋子里的卡片除标有的数字不同外,其大小质地完全相同.
(1)从乙袋里任意抽出一张卡片,抽到标有数字![]() 的概率为 .
的概率为 .
(2)求从甲、乙两个袋子里各抽一张卡片,抽到标有两个数字![]() 的卡片的概率.
的卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AC于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;②![]() ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN=![]() BC,其中正确的是( )
BC,其中正确的是( )
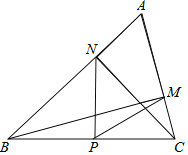
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(﹣2,y2),C(3,y3)都在反比例函数y=![]() (k<0)的图象上,则( )
(k<0)的图象上,则( )
A.y1<y2<y3B.y3<y2<y1C.y3<y1<y2D.y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴相交于A(﹣1,0),B(m,0)两点,与y轴相交于点C(0,﹣3),抛物线的顶点为D.
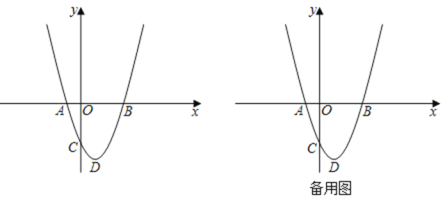
(1)求B、D两点的坐标;
(2)若P是直线BC下方抛物线上任意一点,过点P作PH⊥x轴于点H,与BC交于点M,设F为y轴一动点,当线段PM长度最大时,求PH+HF+![]() CF的最小值;
CF的最小值;
(3)在第(2)问中,当PH+HF+![]() CF取得最小值时,将△OHF绕点O顺时针旋转60°后得到△OH′F′,过点F′作OF′的垂线与x轴交于点Q,点R为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使得点D、Q、R、S为顶点的四边形为菱形,若存在,请直接写出点S的坐标,若不存在,请说明理由.
CF取得最小值时,将△OHF绕点O顺时针旋转60°后得到△OH′F′,过点F′作OF′的垂线与x轴交于点Q,点R为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使得点D、Q、R、S为顶点的四边形为菱形,若存在,请直接写出点S的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开设了![]() :篮球,
:篮球,![]() :足球,
:足球,![]() :跳绳,
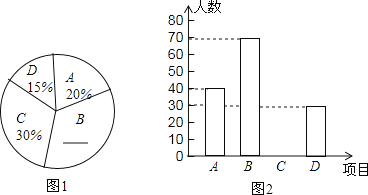
:跳绳,![]() :健美操四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学必须选择而且只能在4中体育活动中选择一种).将数据进行整理并绘制成以下两幅统计图(未画完整).
:健美操四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学必须选择而且只能在4中体育活动中选择一种).将数据进行整理并绘制成以下两幅统计图(未画完整).
(1)这次调查中,一共查了 名学生;
(2)请补全两幅统计图;
(3)若有3名最喜欢足球运动的学生,1名最喜欢跳绳运动的学生组队外出参加一次联谊互动,欲从中选出2人担任组长(不分正副),求两人均是最喜欢足球运动的学生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com