
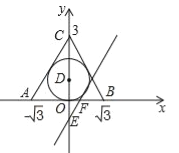
【题目】在平面直角坐标中,△ABC三个顶点坐标为A(﹣![]() ,0)、B(
,0)、B(![]() ,0)、C(0,3).
,0)、C(0,3).
(1)求△ABC内切圆⊙D的半径.
(2)过点E(0,﹣1)的直线与⊙D相切于点F(点F在第一象限),求直线EF的解析式.
(3)以(2)为条件,P为直线EF上一点,以P为圆心,以2![]() 为半径作⊙P.若⊙P上存在一点到△ABC三个顶点的距离相等,求此时圆心P的坐标.
为半径作⊙P.若⊙P上存在一点到△ABC三个顶点的距离相等,求此时圆心P的坐标.
【答案】(1)1;(2)y=![]() x﹣1;(3)若⊙P上存在一点到△ABC三个顶点的距离相等,此时圆心P的坐标为(2
x﹣1;(3)若⊙P上存在一点到△ABC三个顶点的距离相等,此时圆心P的坐标为(2![]() ,5)或(﹣
,5)或(﹣![]() ,﹣4).
,﹣4).
【解析】
试题分析:(1)由A、B、C三点坐标可知∠CBO=60°,又因为点D是△ABC的内心,所以BD平分∠CBO,然后利用锐角三角函数即可求出OD的长度;
(2)根据题意可知,DF为半径,且∠DFE=90°,过点F作FG⊥y轴于点G,求得FG和OG的长度,即可求出点F的坐标,然后将E和F的坐标代入一次函数解析式中,即可求出直线EF的解析式;(3)⊙P上存在一点到△ABC三个顶点的距离相等,该点是△ABC的外接圆圆心,即为点D,所以DP=2![]() ,又因为点P在直线EF上,所以这样的点P共有2个,且由勾股定理可知PF=3
,又因为点P在直线EF上,所以这样的点P共有2个,且由勾股定理可知PF=3![]() .
.
试题解析:(1)连接BD,
∵B(![]() ,0),C(0,3),
,0),C(0,3),
∴OB=![]() ,OC=3,
,OC=3,
∴tan∠CBO![]() ==
==![]() ,
,
∴∠CBO=60°
∵点D是△ABC的内心,
∴BD平分∠CBO,
∴∠DBO=30°,
∴tan∠DBO=![]() ,
,
∴OD=1,
∴△ABC内切圆⊙D的半径为1;
(2)连接DF,
过点F作FG⊥y轴于点G,
∵E(0,﹣1)
∴OE=1,DE=2,
∵直线EF与⊙D相切,
∴∠DFE=90°,DF=1,
∴sin∠DEF=![]() ,
,
∴∠DEF=30°,
∴∠GDF=60°,
∴在Rt△DGF中,
∠DFG=30°,
∴DG=![]() ,
,
由勾股定理可求得:GF=![]() ,
,
∴F(![]() ,
,![]() ),
),
设直线EF的解析式为:y=kx+b,
∴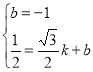 ,
,
∴直线EF的解析式为:y=![]() x﹣1;
x﹣1;
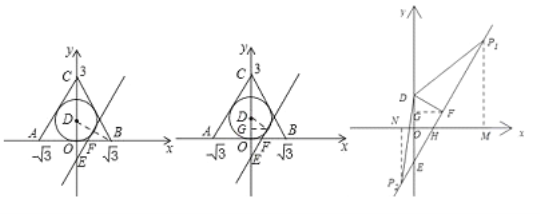
(3)∵⊙P上存在一点到△ABC三个顶点的距离相等,
∴该点必为△ABC外接圆的圆心,
由(1)可知:△ABC是等边三角形,
∴△ABC外接圆的圆心为点D
∴DP=2![]() ,
,
设直线EF与x轴交于点H,
∴令y=0代入y=![]() x﹣1,
x﹣1,
∴x=![]() ,
,
∴H(![]() ,0),
,0),
∴FH=![]() ,
,
当P在x轴上方时,
过点P1作P1M⊥x轴于M,
由勾股定理可求得:P1F=3![]() ,
,
∴P1H=P1F+FH=![]() ,
,
∵∠DEF=∠HP1M=30°,
∴HM![]() =P1H=
=P1H=![]() ,P1M=5,
,P1M=5,
∴OM=2![]() ,
,
∴P1(2![]() ,5),
,5),
当P在x轴下方时,
过点P2作P2N⊥x轴于点N,
由勾股定理可求得:P2F=3![]() ,
,
∴P2H=P2F﹣FH=![]() ,
,
∴∠DEF=30°
∴∠OHE=60°
∴sin∠OHE=![]() ,
,
∴P2N=4,
令y=﹣4代入y=![]() x﹣1,
x﹣1,
∴x=﹣![]() ,
,
∴P2(﹣![]() ,﹣4),
,﹣4),
综上所述,若⊙P上存在一点到△ABC三个顶点的距离相等,此时圆心P的坐标为(2![]() ,5)或(﹣
,5)或(﹣![]() ,﹣4).
,﹣4).


科目:初中数学 来源: 题型:
【题目】有以下两个结论:
① 任何一个有理数和它的相反数之间至少有一个有理数;
② 如果一个有理数有倒数,则这个有理数与它的倒数之间至少有一个有理数。
则( )
A. ①,②都不对; B. ①对,②不对; C. ①,②都对; D. ①不对,②对;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点P(a,b)向上平移3个单位长度,再向左平移2个单位长度后得到的点的坐标是(-2,-3),那么a,b的值分别是( )
A. a=0,b=0 B. a=0,b=-6 C. a=0,b=4 D. a=5,b=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列多项式乘法,不能用平方差公式计算的是( )
A.(-a-b)(-b+a)
B.(xy+z)(xy-z)
C.(-2a-b)(2a+b)
D.(0.5x-y)(-y-0.5x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一元二次方程x2﹣6x+1=0配方成(x+m)2=n的形式,正确的是( )
A. (x+3)2=10 B. (x﹣3)2=10 C. (x+3)2=8 D. (x﹣3)2=8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】启东恒大“海上威尼斯”正在圆陀角风景区全力打造一个完美的“东方威尼斯”,建成后将媲美九大世界著名海湾景区。据福布斯2017年9月19的最新数据显示,恒大集团董事局主席许家印以391亿美元的身价成中国新首富,略高于马化腾和马云。391亿用科学记数法表示为( )
A. 3.91×108 B. 3.91×109 C. 3.91×1010 D. 3.91×1011
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com