
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC和△A1B1C1关于x轴成轴对称,画出△A1B1C1
(2)点C1的坐标为_________,△ABC的面积为__________.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了更好治理西太湖水质,保护环境,市治污公司决定购买10台污水处理设备,现有A、B两种型号的设备,其中每台的价格,月处理污水量如下表:

经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买4台B型设备少4万元.
(1)求a、b的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过47万元,你认为该公司有哪几种购买方案;
(3)在(2)问的条件下,若该月要求处理西太湖的污水量不低于1860吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
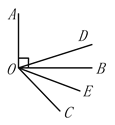
【题目】如图,DO平分∠AOC,OE平分∠BOC,若OA⊥OB,
(1)当∠BOC=30°,∠DOE=_______________; 当∠BOC=60°,∠DOE=_______________;
(2)通过上面的计算,猜想∠DOE的度数与∠AOB有什么关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在平时的练习中,遇到下面一道题目:
如图,∠AOC=90°,OE 平分∠BOC,OD平分∠AOB.
①若∠BOC=60°,求∠DOE 度数;
②若∠BOC=α(0<α<90°),其他条件不变,求∠DOE 的度数.
(1)下面是某同学对①问的部分解答过程,请你补充完整.
∵OE 平分∠BOC,∠BOC=60°
∴∠BOE= . (角平分线的定义)
∵∠AOC=90°,∠BOC=60°
∴ ,
∵OD 平分∠AOB,
∴ ,(角平分线的定义)
∴∠DOE= .
(注:符号∵表示因为,用符号∴表示所以).
(2)仿照①的解答过程,完成第②小题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与
与 ![]() 轴交于点
轴交于点 ![]() (点
(点 ![]() 分别在
分别在 ![]() 轴的左右两侧)两点,与
轴的左右两侧)两点,与 ![]() 轴的正半轴交于点
轴的正半轴交于点 ![]() ,顶点为
,顶点为 ![]() ,已知点
,已知点 ![]() .
.
(1)求点 ![]() 的坐标;
的坐标;
(2)判断△ ![]() 的形状,并说明理由;
的形状,并说明理由;
(3)将△ ![]() 沿
沿 ![]() 轴向右平移
轴向右平移 ![]() 个单位(
个单位( ![]() )得到△
)得到△ ![]() .△
.△ ![]() 与△
与△ ![]() 重叠部分(如图中阴影)面积为
重叠部分(如图中阴影)面积为 ![]() ,求
,求 ![]() 与
与 ![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l1:![]() 与坐标轴交于A,B两点,直线l2:
与坐标轴交于A,B两点,直线l2:![]() (
(![]() ≠0)与坐标轴交于点C,D.
≠0)与坐标轴交于点C,D.
(1)求点A,B的坐标;
(2)如图,当![]() =2时,直线l1,l2与相交于点E,求两条直线与
=2时,直线l1,l2与相交于点E,求两条直线与![]() 轴围成的△BDE的面积;
轴围成的△BDE的面积;
(3)若直线l1,l2与![]() 轴不能围成三角形,点P(a,b)在直线l2:
轴不能围成三角形,点P(a,b)在直线l2:![]() (k≠0)上,且点P在第一象限.
(k≠0)上,且点P在第一象限.
①求![]() 的值;
的值;
②若![]() ,,求
,,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板放在同一平面内,使直角顶点重合于点O
(1)如图①,若∠AOB=155°,求∠AOD、∠BOC、∠DOC的度数.
(2)如图①,你发现∠AOD与∠BOC的大小有何关系?∠AOB与∠DOC有何关系?直接写出你发现的结论.
(3)如图②,当△AOC与△BOD没有重合部分时,(2)中你发现的结论是否还仍然成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员 | 小丽 | 小华 |
月销售件数(件) | 200 | 150 |
月总收入(元) | 1400 | 1250 |
假设营业员的月基本工资为x元,销售每件服装奖励y元.
(1)求x、y的值;
(2)若营业员小丽某月的总收入不低于1800元,那么小丽当月至少要卖服装多少件?
(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需315元;如果购买甲1件,乙2件,丙3件共需285元.某顾客想购买甲、乙、丙各一件共需 元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com