
| A地 | B地 | C地 | |
| 运往甲县的费用(元/吨) | 220 | 200 | 200 |
| 运往乙县的费用(元/吨) | 250 | 220 | 210 |
分析 (1)设这批赈灾物资运往乙县的数量是a吨,则运往甲县的数量是(2a-20)吨,根据A、B、C三地分别有赈灾物资100吨、100吨、80吨,说明赈灾物资一共有280吨,根据等量关系式:运往甲县的数量+运往乙县的数量=280列方程解出.
(2)由A地→甲县x吨,C地→甲县60吨,可知B地→甲县(180-60-x)吨,A地→乙县(100-x)吨,C地→乙县80-60=20吨,B地→乙县[100-(180-60-x)]吨;根据B地→甲县数量<A地→甲县数量的2倍得:180-60-x<2x;根据B地→乙县数量不超过25吨得:100-(180-60-x)≤25;列不等式组求整数解.
(3)设总费用为w元,表示出w的值,化成一次函数,利用增减性求最大值.
解答 解:(1)设这批赈灾物资运往乙县的数量是a吨,则运往甲县的数量是(2a-20)吨,
则a+2a-20=100+100+80,
a=100,
2a-20=2×100-20=180,
答:这批赈灾物资运往甲、乙两县的数量分别是180吨、100吨.
(2)根据题意得:$\left\{\begin{array}{l}{180-60-x<2x①}\\{100-(180-60-x)≤25②}\end{array}\right.$,
解①得:x>40,
解②得:x≤45,
∴不等式组的解集为:40<x≤45,
整数解为:41、42、43、44、45;
则A、B两地的赈灾物资运往甲、乙两县的方案有五种;
(3)设总费用为w元,
则w=220x+250(100-x)+200(180-60-x)+220(x-20)+200×60+210×20,
w=-10x+60800,
∵-10<0,
∴w随x的增大而减小,
∴当x=41时,w有最大值,w大=-10×41+60800=60390,
答:该公司承担运送这批赈灾物资的总费用最多是60390元.
点评 本题主要考查了一元一次不等式组的应用和一次函数的最值问题,把函数和应用题结合起来,是数学中的一个难点,理解是关键;本题的第一问是运用一元一次方程来求解,也可以利用二元一次方程组求解;在应用题中求最值问题,可以把它转化为函数求最值问题,这个解题思路常用.


科目:初中数学 来源: 题型:选择题
 如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为( )
如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为( )| A. | 85° | B. | 70° | C. | 75° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
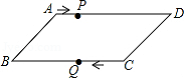 如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm 的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有3次.
如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD边上以每秒1cm 的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有3次.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8.18×108 | B. | 81.8×109 | C. | 8.18×1010 | D. | 0.818×109 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com