
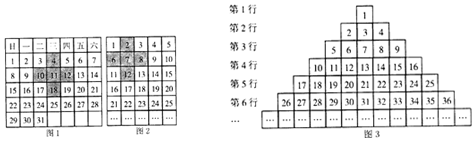
分析 (1)根据题意求出相应的“十字差”,即可确定出所求定值;
(2)定值为k2-1=(k+1)(k-1),理由为:设十字星中心的数为x,表示出十字星左右两数,上下两数,进而表示出十字差,化简即可得证;
(3)设正中间的数为a,则上下两个数为a-62,a+64,左右两个数为a-1,a+1,根据相应的“十字差”为2017求出a的值即可.
解答 解:(1)根据题意得:6×8-2×12=48-24=24;
故答案为:24;
(2)定值为k2-1=(k+1)(k-1);
证明:设十字星中心的数为x,则十字星左右两数分别为x-1,x+1,上下两数分别为x-k,x+k(k≥3),
十字差为(x-1)(x+1)-(x-k)(x+k)=x2-1-x2+k2=k2-1,
故这个定值为k2-1=(k+1)(k-1);
(3)设正中间的数为a,则上下两个数为a-62,a+64,左右两个数为a-1,a+1,
根据题意得:(a-1)(a+1)-(a-62)(a+64)=2017,
解得:a=975.
故答案为:975.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三角形的外角中至少有两个是钝角 | B. | 直角三角形的两锐角互余 | ||
| C. | 全等三角形的对应边相等 | D. | 当m=1时,分式$\frac{|m|-1}{{m}^{2}-m}$的值为零 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com