
 如图,AC为⊙O的直径,PA切⊙O于点A,点B为⊙O上一点,PB与AC的延长线交于点D,连接OB,∠COB=∠APB,连接OP.
如图,AC为⊙O的直径,PA切⊙O于点A,点B为⊙O上一点,PB与AC的延长线交于点D,连接OB,∠COB=∠APB,连接OP.分析 (1)根据切线的性质得到∠A=90°,根据相似三角形的性质得到结论;
(2)根据勾股定理得到AP=$\sqrt{O{P}^{2}-O{A}^{2}}$=6$\sqrt{2}$,根据相似三角形的性质得到$\frac{OB}{AP}=\frac{BD}{AD}$=$\frac{1}{2}$,求得AD=2BD,设BD=x,OD=2x-3$\sqrt{3}$,根据勾股定理列方程即可得到结论.
解答 解:(1)∵AC为⊙O的直径,PA切⊙O于点A,
∴∠A=90°,
∵∠COB=∠APB,∠D=∠D,
∴△DBO∽△DAP,
∴∠DBO=∠PAD=90°,
∴OB⊥PD,
∴PB为⊙O的切线;
(2)∵OP=3$\sqrt{10}$,OC=3$\sqrt{2}$,
∴OA=OC=3$\sqrt{2}$,
∴AP=$\sqrt{O{P}^{2}-O{A}^{2}}$=6$\sqrt{2}$,∵△DBO∽△DAP,
∴$\frac{OB}{AP}=\frac{BD}{AD}$=$\frac{1}{2}$,
∴AD=2BD,
设BD=x,OD=2x-3$\sqrt{3}$,
∵OB2+BD2=OD2,
即(3$\sqrt{2}$)2+x2=(2x-3$\sqrt{2}$)2,
∴x=4$\sqrt{2}$,
∴BD=4$\sqrt{2}$,OD=5$\sqrt{2}$,
∴CD=2$\sqrt{2}$.
点评 本题考查了切线的性质,勾股定理,相似三角形的判定和性质,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
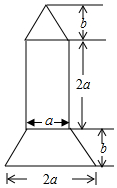 2016年9月15日晚,正值中秋佳节,我国“天宫二号”空间实验室顺利升空.同学们倍受鼓舞,某同学绘制了如图所示的火箭模型截面图,下面是梯形,中间是长方形,上面是三角形.
2016年9月15日晚,正值中秋佳节,我国“天宫二号”空间实验室顺利升空.同学们倍受鼓舞,某同学绘制了如图所示的火箭模型截面图,下面是梯形,中间是长方形,上面是三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
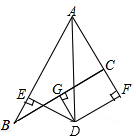 已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
已知:如图∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
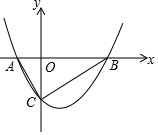 如图,抛物线y=$\frac{1}{2}$x2-x+a与x轴交于点A、B,与y轴交于点C,其顶点纵坐标为-2.
如图,抛物线y=$\frac{1}{2}$x2-x+a与x轴交于点A、B,与y轴交于点C,其顶点纵坐标为-2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com