
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义: 如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1 , A2B2C2D2 , AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.
(1)已知A(﹣2,3),B(5,0),C(t,﹣2). ①当t=2时,点A,B,C的最优覆盖矩形的面积为;
②若点A,B,C的最优覆盖矩形的面积为40,求直线AC的表达式;
(2)已知点D(1,1).E(m,n)是函数y= ![]() (x>0)的图象上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
(x>0)的图象上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
【答案】
(1)35;②∵点A,B,C的最优覆盖矩形的面积为40, ∴由定义可知,t=﹣3或6,即点C坐标为(﹣3,﹣2)或(6,﹣2),
设AC表达式为y=kx+b,
∴ ![]() 或
或 ![]()
∴ ![]() 或
或 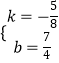
∴y=5x+13或 ![]()
(2)①OD所在的直线交双曲线于点E,矩形OFEG是点O,D,E的一个面积最小的最优覆盖矩形,如图1所示:
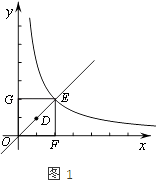
∵点D(1,1),
∴OD所在的直线表达式为y=x,
∴点E的坐标为(2,2),
∴OE= ![]() =
= ![]() ,
,
∴⊙H的半径最小r= ![]() ,
,
②当点E的纵坐标为1时,如图2所示:
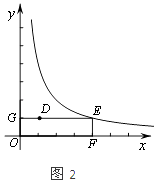
1= ![]() ,解得x=4,
,解得x=4,
∴OE═ ![]() =
= ![]() ,
,
∴⊙H的半径最大r= ![]() ,
,
∴ ![]() .
.
【解析】解:(1)①∵A(﹣2,3),B(5,0),C(2,﹣2),矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形, ∴最优覆盖矩形的长为:2+5=7,宽为3+2=5,
∴最优覆盖矩形的面积为:7×5=35;


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】课题学习:设计概率模拟实验. 在学习概率时,老师说:“掷一枚质地均匀的硬币,大量重复实验后,正面朝上的概率约是 ![]() .”小海、小东、小英分别设计了下列三个模拟实验:
.”小海、小东、小英分别设计了下列三个模拟实验:
小海找来一个啤酒瓶盖(如图1)进行大量重复抛掷,然后计算瓶盖口朝上的次数与总次数的比值;
小东用硬纸片做了一个圆形转盘,转盘上分成8个大小一样的扇形区域,并依次标上1至8个数字(如图2),转动转盘10次,然后计算指针落在奇数区域的次数与总次数的比值;
小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子(如图3),其中有三枚是白子,一枚是黑子,从中随机同时摸出两枚棋子,并大量重复上述实验,然后计算摸出的两枚棋子颜色不同的次数与总次数的比值.
根据以上材料回答问题:
小海、小东、小英三人中,哪一位同学的实验设计比较合理,并简要说出其他两位同学实验的不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长
最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+ ![]() )(x>0).
)(x>0).
【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+ ![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数y=x+ ![]() 的自变量x的取值范围是x>0,如表是y与x的几组对应值.
的自变量x的取值范围是x>0,如表是y与x的几组对应值.
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①写出m的值;
②画出该函数图象,结合图象,得出当x=时,y有最小值,y最小=;
(2)【解决问题】
直接写出“问题情境”中问题的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
![]() ……
……
(1)请写出第4个等式:________________;
(2)观察上述等式的规律,猜想第n个等式(用含n的式子表示),并验证其正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
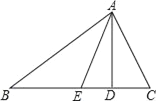
【题目】如图,AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=70°,分别求:
(1)∠BAC的度数;
(2)∠AED的度数;
(3)∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形![]() 中,
中,![]() =4cm,
=4cm,![]() =3cm,
=3cm,![]() 为
为![]() 的中点.动点
的中点.动点![]() 从
从![]() 点出发,以每秒1cm的速度沿
点出发,以每秒1cm的速度沿![]() 运动,最终到达点
运动,最终到达点![]() .若点
.若点![]() 运动的时间为
运动的时间为![]() 秒,则当
秒,则当![]() =________ 时,
=________ 时,![]() 的面积等于4.5.
的面积等于4.5.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,m)在边AB上,反比例函数y= ![]() (k≠0)在第一象限内的图象经过点D、E,且cos∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且cos∠BOA= ![]() .
.
(1)求边AB的长;
(2)求反比例函数的解析式和m的值;
(3)若反比例函数的图象与矩形的边BC交于点F,点G、H分别是y轴、x轴上的点,当△OGH≌△FGH时,求线段OG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com