
【题目】如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).
(1)直接写出点E的坐标;
(2)在四边形ABCD中,点P从点B出发,沿“BC→CD”移动.若点P的速度为每秒1个单位长度,运动时间为t秒,回答下列问题:
①当t等于多少秒时,点P的横坐标与纵坐标互为相反数;
②求点P在运动过程中的坐标,(用含t的式子表示,写出过程);
③当3秒<t<5秒时,设∠CBP=x°,∠PAD=y°,∠BPA=z°,用含x,y的式子表示z.
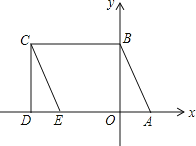
【答案】(1)点E的坐标是(﹣2,0);(2)①当t=2秒时,点P的横坐标与纵坐标互为相反数;②当点P在线段BC上时,点P的坐标(﹣t,2),当点P在线段CD上时,点P的坐标(﹣3,5﹣t);③能确定,z=x+y.
【解析】
(1)根据平移的性质即可得到结论;
(2)①由点C的坐标为(﹣3,2).得到BC=3,CD=2,由于点P的横坐标与纵坐标互为相反数;于是确定点P在线段BC上,有PB=CD,即可得到结果;
②分两种情况讨论:当点P在线段BC上时;当点P在线段CD上时;
③如图,过P作PF∥BC交AB于F,则PF∥AD,根据平行线的性质即可得到结论.
(1)根据题意,可知:三角形OAB沿x轴负方向平移3个单位得到三角形DEC.
∵点A的坐标是(1,0),∴点E的坐标是(﹣2,0).
(2)①∵点C的坐标为(﹣3,2),∴BC=3,CD=2.
∵点P的横坐标与纵坐标互为相反数,∴点P在线段BC上,∴PB=CD,即t=2,∴当t=2秒时,点P的横坐标与纵坐标互为相反数.
②当点P在线段BC上时,点P的坐标(﹣t,2);
当点P在线段CD上时,点P的坐标(﹣3,5﹣t);
③能确定,如图,过P作PF∥BC交AB于F,则PF∥AD,∴∠1=∠CBP=x°,∠2=∠DAP=y°,∴∠BPA=∠1+∠2=x°+y°=z°,∴z=x+y.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】填写推理理由,将过程补充完整:
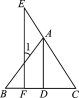
如图,已知AD⊥BC于点D,EF⊥BC于点F,AD平分∠BAC.求证:∠E=∠1.
证明:∵AD⊥BC,EF⊥BC(已知),
∴∠ADC=∠EFC=90°(垂直的定义).
∴____________(_____________).
∴∠1=_____(_____________),
∠E=_____(_______________).
又∵AD平分∠BAC(已知),
∴_____=________.
∴∠1=∠E(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答问题:
分解因式:x3+3x2-4.
解答:把x=1代入多项式x3+3x2-4,发现此多项式的值为0,由此确定多项式x3+3x2-4中有因式(x-1),于是可设x3+3x2-4=(x-1)(x2+mx+n),分别求出m,n的值,再代入x3+3x2-4=(x-1)(x2+mx+n),就容易分解多项式x3+3x2-4.这种分解因式的方法叫“试根法”.
(1)求上述式子中m,n的值;
(2)请你用“试根法”分解因式:x3+x2-16x-16.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,若按图中规律继续下去,则∠1+∠2+…+∠n等于( )
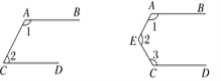

A. n·180° B. 2n·180° C. (n-1)·180° D. (n-1)2·180°
查看答案和解析>>
科目:初中数学 来源: 题型:
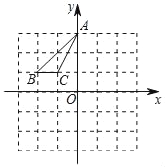
【题目】如图,在平面直角坐标系中,三角形ABC的顶点A、B、C的坐标分别为(0,3)、(﹣2,1)、(﹣1,1),如果将三角形ABC先向右平移2个单位长度,再向下平移2个单位长度,会得到三角形A′B′C′,点A'、B′、C′分别为点A、B、C移动后的对应点.
(1)请直接写出点A′、B'、C′的坐标;
(2)请在图中画出三角形A′B′C′,并直接写出三角形A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪下全等的四块小长方形,然后按图2拼成一个正方形.
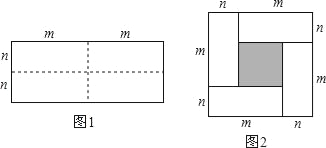
(1)直接写出图2中的阴影部分面积;
(2)观察图2,请直接写出下列三个代数式(m+n)2,(m﹣n)2,mn之间的等量关系;
(3)根据(2)中的等量关系,解决如下问题:若p+q=9,pq=7,求(p﹣q)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售A、B两种不同型号的电风扇,每种型号电风扇的购买单价分别为每台310元,460元.
(1)若某单位购买A,B两种型号的电风扇共50台,且恰好支出20000元,求A,B两种型号电风扇各购买多少台?
(2)若购买A,B两种型号的电风扇共50台,且支出不超过18000元,求A种型号电风扇至少要购买多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:
计算代数式![]() (其中x≠0)的值后填入下表.并根据表格所反映出的
(其中x≠0)的值后填入下表.并根据表格所反映出的![]() (其中x≠0)的值与x之间的变化规律进行探究.
(其中x≠0)的值与x之间的变化规律进行探究.
x | …… | 0.25 | 0.5 | 1 | 10 | 100 | 1000 | 10000 | …… |
| …… | …… |
下面是小东计算代数式![]() (其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:
(其中x≠0)的值后填入表格,并根据表格进行探究的过程,请补充完整:
x | …… | 0.25 | 0.5 | 1 | 10 | 100 | 1000 | 10000 | …… |
| …… | 2 | 1 |
|
|
|
| …… |
(1)上表是![]() (其中x≠0)与x的几组对应值.直接写出x=10时,求代数式
(其中x≠0)与x的几组对应值.直接写出x=10时,求代数式![]() 的值;
的值;
(2)随着x值的增大,代数式![]() 的值有何变化(回答“增大”或“减少”);
的值有何变化(回答“增大”或“减少”);
(3)当x值无限增大时,代数式![]() 的值无限趋近于一个数,这个数是多少.
的值无限趋近于一个数,这个数是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com