
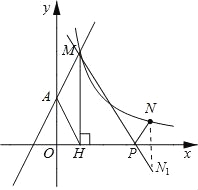
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数y=![]() (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)4;(2)存在,P点坐标为(![]() ,0).
,0).
【解析】
试题分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置.
试题解析:(1)由y=2x+2可知A(0,2),即OA=2.∵tan∠AHO=2,∴OH=1.∵MH⊥x轴,∴点M的横坐标为1.∵点M在直线y=2x+2上,∴点M的纵坐标为4.即M(1,4).∵点M在y=![]() 上,∴k=1×4=4.(2)存在.过点N作N关于x轴的对称点N1,连接MN1,交x轴于P(如图所示).此时PM+PN最小.∵点N(a,1)在反比例函数y=
上,∴k=1×4=4.(2)存在.过点N作N关于x轴的对称点N1,连接MN1,交x轴于P(如图所示).此时PM+PN最小.∵点N(a,1)在反比例函数y=![]() (x>0)上,∴a=4.即点N的坐标为(4,1).∵N与N1关于x轴的对称,N点坐标为(4,1),∴N1的坐标为(4,﹣1).设直线MN1的解析式为y=kx+b.由
(x>0)上,∴a=4.即点N的坐标为(4,1).∵N与N1关于x轴的对称,N点坐标为(4,1),∴N1的坐标为(4,﹣1).设直线MN1的解析式为y=kx+b.由![]() 解得k=﹣
解得k=﹣![]() ,b=
,b=![]() .∴直线MN1的解析式为y=﹣
.∴直线MN1的解析式为y=﹣![]() x+
x+![]() .令y=0,得x=
.令y=0,得x=![]() .∴P点坐标为(
.∴P点坐标为(![]() ,0).
,0).


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
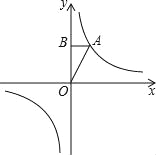
【题目】如图,已知反比例函数y=![]() (k>0)的图象经过点A(1,m),过点A作AB⊥y轴于点B,且△AOB的面积为1.
(k>0)的图象经过点A(1,m),过点A作AB⊥y轴于点B,且△AOB的面积为1.
(1)求m,k的值;
(2)若一次函数y=nx+2(n≠0)的图象与反比例函数y=![]() 的图象有两个不同的公共点,求实数n的取值范围.
的图象有两个不同的公共点,求实数n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各题中的数是准确数的是( ).
A.初一年级有400名同学
B.月球与地球的距离约为38万千米
C.毛毛身高大约158㎝
D.今天气温估计30℃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有9名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前4名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这9名同学成绩的( )
A. 平均数B. 方差C. 中位数D. 极差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.在同一年出生的400人中至少有两人的生日相同
B.投掷一粒骰子,连投两次点数相同的概率与连投两次点数都为1的概率是相等的
C.从一副完整的扑克牌中随机抽取一张牌恰好是红桃K,这是必然事件
D.一个袋中装有3个红球,5个白球,任意摸出一个球是红球的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=∠COD=90°, 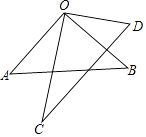
(1)指出图中以点O为顶点的角中,互为补角的角并说明理由.
(2)若∠COB= ![]() ∠AOD,求∠AOD的度数.
∠AOD,求∠AOD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com