
【题目】如图,已知二次函数y1=ax2+bx+c的图象过点A(1,0),B(﹣3,0),C(0,﹣3) 
(1)求此二次函数的解析式和顶点坐标;
(2)直线y2=kx+b过B、C两点,请直接写出当y1>y2时,自变量x的取值范围.
【答案】
(1)解:∵二次函数y1=ax2+bx+c的图象过点A(1,0),B(﹣3,0),C(0,﹣3),
∴  ,解得
,解得  ,
,
∴二次函数的解析式为:y=x2+2x﹣3,顶点坐标为(﹣1,﹣4)
(2)解:∵B(﹣3,0),C(0,﹣3),
∴当y1>y2时,x<﹣3或x>0
【解析】(1)直接利用待定系数法求出二次函数的解析式,再求出其顶点坐标即可;(2)根据函数图象即可得出结论.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是边BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③四边形AEPF的面积=△ABC的面积的一半,④当EF最短时,EF=AP,上述结论始终正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
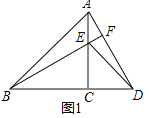
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF= ![]() AB.
AB.
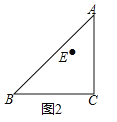
(3)如图3,若∠EDF的两边分别交AB,AC的延长线于E、F两点,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BE,AB,CF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=22°,则∠B的度数是( ) 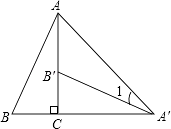
A.67°
B.62°
C.82°
D.72°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
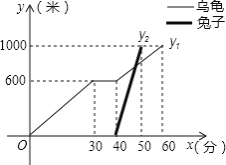
①兔子和乌龟同时从起点出发;
②“龟兔再次赛跑”的路程为1000米;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法共有____________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到离A的距离等于___________时,ΔABC和ΔPQA全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,
,![]() 在线段
在线段![]() 上,连接
上,连接![]() ,
,![]() 的延长线交
的延长线交![]() 于
于![]() .
.
(1)猜想线段![]() 、
、![]() 的关系;(不必证明)
的关系;(不必证明)
(2)当点![]() 为
为![]() 内部一点时,使点
内部一点时,使点![]() 和点
和点![]() 分别在
分别在![]() 的两侧,其它条件不变.请你在图2中补全图形,则(1)中结论成立吗?若成立,请证明;若不成立,请说明理由.
的两侧,其它条件不变.请你在图2中补全图形,则(1)中结论成立吗?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com