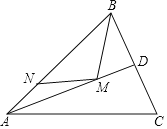
【题目】如图，在锐角△ABC中，AB=5
，∠BAC=45°，∠BAC的平分线交BC于点D，M，N分别是AD，AB上的动点，则BM+MN的最小值是______．
科目：初中数学 来源： 题型：
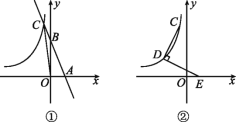
【题目】如图①，直线y=-2x+4交x轴、y轴于A，B两点，交双曲线y=
(x<0)于C点，△OAC的面积为6．
(1)求双曲线的解析式；
(2)如图②，D为双曲线y=(x<0)上一点，连接CD，将线段CD绕点D顺时针旋转90°得线段DE，点E恰好落在x轴上，求点E的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
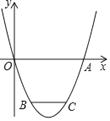
【题目】已知开口向上的抛物线
交
轴于点
，
，函数值
的最小值是
．
（1）求抛物线的解析式．
（2）点
为抛物线上的点，并在对称轴的左侧．作
轴交抛物线于点
，连结
，
，且
．
①求
的值．
②若点
在线段上，以点为圆心，
为半径画圆．当
和
的一边相切时，求点的横坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了推进球类运动的发展，某校组织校内球类运动会，分篮球、足球、排球、羽毛球、乒乓球五项，要求每位学生必须参加一项并且只能参加一项，某班有一名学生根据自己了解的班内情况绘制了如图所示的不完整统计表和扇形统计图.
请根据图表中提供的信息，解答下列问题：
（1）图表中m=________，n=________；
（2）若该校学生共有1000人，则该校参加羽毛球活动的人数约为________人；
（3）该班参加乒乓球活动的4位同学中，有3位男同学（分别用A，B，C表示）和1位女同学（用D表示），现准备从中选出两名同学参加双打比赛，用树状图或列表法求出恰好选出一男一女的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】今年5月，某大型商业集团随机抽取所属的部分商业连锁店进行评估，将抽取的各商业连锁店按照评估成绩分成了
、
、
、
四个等级，并绘制了如下不完整的扇形统计图和条形统计图.
根据以上信息，解答下列问题：
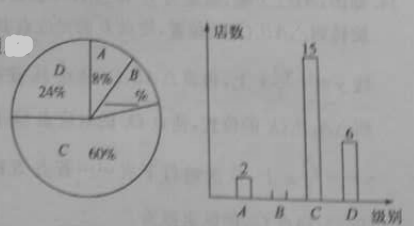
（1）本次评估随机抽取了多少家商业连锁店？
（2）请补充完整扇形统计图和条形统计图，并在图中标注相应数据；
（3）从、两个等级的商业连锁店中任选2家介绍营销经验，求其中至少有一家是等级的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某经销商销售一种成本价为10元/kg的商品，已知销售价不低于成本价，且物价部门规定这种产品的销售价不得高于18元/kg．在销售过程中发现销量y（kg）与售价x（元/kg）之间满足一次函数关系，对应关系如下表所示：
⑴求y与x之间的函数关系式，并写出自变量x的取值范围；
⑵若该经销商想使这种商品获得平均每天168元的利润，求售价应定为多少元/kg？
⑶设销售这种商品每天所获得的利润为W元，求W与x之间的函数关系式；并求出该商品销售单价定为多少元时，才能使经销商所获利润最大？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在某温度不变的条件下，通过一次又一次地对气缸顶部的活塞加压，测出每一次加压后气缸内气体的体积
与气体对气缸壁产生的压强
的关系可以用如图所示的函数图象进行表示，下列说法正确的是（ ）
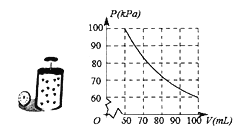
A.气压P与体积V的关系式为
B.当气压
时，体积V的取值范围为
C.当体积V变为原来的一半时，对应的气压P也变为原来的一半
D.当
时，气压P随着体积V的增大而减小
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点I为△ABC的内心，AB=4，AC=3，BC=2，将∠ACB平移使其顶点与I重合，则图中阴影部分的周长为（ ）
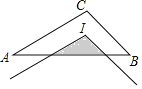
A. 4.5 B. 4 C. 3 D. 2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线经过 A、B、C 三点，其中 A(0，3)，B(﹣1，0)，且∠ACO＝45°；
（1）求抛物解析式；
（2）点 P 为线段 AC 上方抛物线上一动点，过 P 作 PQ∥AB 分别交 AC、x 轴于 F、Q 两点， 过 P 作 PD⊥x 轴分别交 AC、x 轴于 E、D 两点，且 S△CFQ＝3S△PEF；①
的值；②求 F 点坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
