
”¾ĢāÄæ”æĢ½¾æÓė·¢ĻÖ£ŗČēĶ¼1ĖłŹ¾µÄĶ¼ŠĪ£¬ĻńĪŅĆĒ³£¼ūµÄѧĻ°ÓĆĘ·©©Ō²¹ę£®ĪŅĆĒ²»·Į°ŃÕāŃłĶ¼ŠĪ½Š×ö”°¹ęŠĪĶ¼”±£®
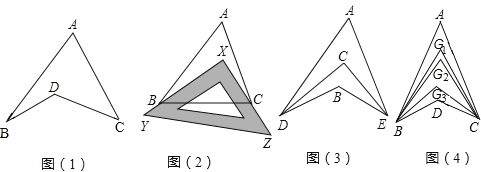
£Ø1£©¹Ū²ģ”°¹ęŠĪĶ¼”±£¬ŹŌĢ½¾æ”ĻBDCÓė”ĻA”¢”ĻB”¢”ĻCÖ®¼äµÄ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø2£©ĒėÄćÖ±½ÓĄūÓĆŅŌÉĻ½įĀŪ£¬½ā¾öŅŌĻĀČżøöĪŹĢā£ŗ
¢ŁČēĶ¼2£¬°ŃŅ»æéČż½Ē³ßXYZ·ÅÖĆŌŚ”÷ABCÉĻ£¬Ź¹Čż½Ē³ßµÄĮ½ĢõÖ±½Ē±ßXY”¢XZĒ”ŗĆ¾¹żµćB”¢C£¬”ĻA=40”ć£¬Ōņ”ĻABX+”ĻACX=”” ”””ć£»
¢ŚČēĶ¼3£¬DCĘ½·Ö”ĻADB£¬ECĘ½·Ö”ĻAEB£¬Čō”ĻDAE=40”ć£¬”ĻDBE=130”ć£¬Ēó”ĻDCEµÄ¶ČŹż£»
¢ŪČēĶ¼4£¬”ĻABD£¬”ĻACDµÄ10µČ·ÖĻßĻą½»ÓŚµćG1”¢G2””¢G9£¬Čō”ĻBDC=133”ć£¬”ĻBG1C=70”ć£¬Ēó”ĻAµÄ¶ČŹż£®
”¾“š°ø”æ£Ø1£©”ĻBDC=”ĻA+”ĻB+”ĻC£»£Ø2£©¢Ł50”ć£»¢Ś85”ć£»¢Ū63”ć.
”¾½āĪö”æ
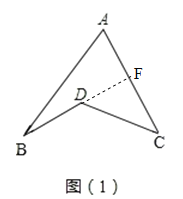
£Ø1£©ŃÓ³¤BD½»ACÓŚF£¬øł¾ŻĶā½ĒµÄŠŌÖŹ£¬¼“æÉÅŠ¶Ļ³ö”ĻBDC=”ĻBAC+”ĻB+”ĻC£®
£Ø2£©¢ŁÓÉ£Ø1£©æɵƔĻABX+”ĻACX+”ĻA=”ĻBXC£¬Č»ŗóøł¾Ż”ĻA=40”ć£¬”ĻBXC=90”ć£¬¼“æÉĒó³ö”ĻABX+”ĻACXµÄÖµ£®
¢ŚÓÉ£Ø1£©æɵƔĻDBE=”ĻDAE+”ĻADB+”ĻAEB£¬ŌŁøł¾Ż”ĻDAE=40”ć£¬”ĻDBE=130”ć£¬Ēó³ö”ĻADB+”ĻAEBµÄÖµ£»Č»ŗóøł¾Ż”ĻDCE![]() £Ø”ĻADB+”ĻAEB£©+”ĻDAE£¬¼“æÉĒó³ö”ĻDCEµÄ¶ČŹż£®
£Ø”ĻADB+”ĻAEB£©+”ĻDAE£¬¼“æÉĒó³ö”ĻDCEµÄ¶ČŹż£®
¢Ūøł¾Ż”ĻBG1C![]() £Ø”ĻABD+”ĻACD£©+”ĻA£¬”ĻBG1C=70”ć£¬Éč”ĻAĪŖx”ć£¬æɵƔĻABD+”ĻACD=133”ć©x”ć£¬½ā·½³Ģ£¬Ēó³öxµÄÖµ£¬¼“æÉÅŠ¶Ļ³ö”ĻAµÄ¶ČŹż£®
£Ø”ĻABD+”ĻACD£©+”ĻA£¬”ĻBG1C=70”ć£¬Éč”ĻAĪŖx”ć£¬æɵƔĻABD+”ĻACD=133”ć©x”ć£¬½ā·½³Ģ£¬Ēó³öxµÄÖµ£¬¼“æÉÅŠ¶Ļ³ö”ĻAµÄ¶ČŹż£®
£Ø1£©ČēĶ¼£Ø1£©£¬ŃÓ³¤BD½»ACÓŚF£¬øł¾ŻĶā½ĒµÄŠŌÖŹ£¬æÉµĆ£ŗ”ĻDFC=”ĻA+”ĻB£®
”ß”ĻBDC=”ĻDFC+”ĻC£¬”ą”ĻBDC=”ĻA+”ĻB+”ĻC£»
£Ø2£©¢ŁÓÉ£Ø1£©£¬æÉµĆ£ŗ”ĻABX+”ĻACX+”ĻA=”ĻBXC£®
”ß”ĻA=40”ć£¬”ĻBXC=90”ć£¬”ą”ĻABX+”ĻACX=90”ć©40”ć=50”ć£®
¹Ź“š°øĪŖ£ŗ50£®
¢ŚÓÉ£Ø1£©£¬æÉµĆ£ŗ”ĻDBE=”ĻDAE+”ĻADB+”ĻAEB£¬”ą”ĻADB+”ĻAEB=”ĻDBE©”ĻDAE=130”ć©40”ć=90”ć£¬”ą![]() £Ø”ĻADB+”ĻAEB£©=90”ć”Ā2=45”ć£¬”ą”ĻDCE
£Ø”ĻADB+”ĻAEB£©=90”ć”Ā2=45”ć£¬”ą”ĻDCE![]() £Ø”ĻADB+”ĻAEB£©+”ĻDAE=45”ć+40”ć=85”ć£»
£Ø”ĻADB+”ĻAEB£©+”ĻDAE=45”ć+40”ć=85”ć£»
¢Ū”ĻBG1C![]() £Ø”ĻABD+”ĻACD£©+”ĻA£®
£Ø”ĻABD+”ĻACD£©+”ĻA£®
”ß”ĻBG1C=70”ć£¬”ąÉč”ĻAĪŖx”ć£®
”ß”ĻABD+”ĻACD=133”ć©x”ć
”ą![]() £Ø133©x£©+x=70£¬”ą13.3
£Ø133©x£©+x=70£¬”ą13.3![]() x+x=70£¬½āµĆ£ŗx=63£¬¼“”ĻAµÄ¶ČŹżĪŖ63”ć£®
x+x=70£¬½āµĆ£ŗx=63£¬¼“”ĻAµÄ¶ČŹżĪŖ63”ć£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćA£¬BµÄ×ų±ź·Ö±šĪŖ£Ø1£¬4£©ŗĶ£Ø4£¬4£©£¬Å×ĪļĻßy=a£Øx+m£©2+nµÄ¶„µćŌŚĻ߶ĪABÉĻ£¬ÓėxÖį½»ÓŚC£¬DĮ½µć£ØCŌŚDµÄ×ó²ą£©£¬µćCµÄŗį×ų±ź×īŠ”ÖµĪŖ©3£¬ŌņµćDµÄŗį×ų±źµÄ×ī“óÖµĪŖ £® 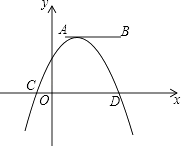
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĆæøöŠ”Õż·½ŠĪµÄ±ß³¤ĪŖ1£¬ŌŚ·½øńÖ½ÄŚ½«”÷ABC¾¹żŅ»“ĪĘ½ŅĘŗóµĆµ½”÷A”äB”äC”䣬Ķ¼ÖŠ±ź³öĮĖµćBµÄ¶ŌÓ¦µćB”䣬ĄūÓĆĶųøńµć»Ķ¼ŗĶĪŽæĢ¶ČµÄÖ±³ß»Ķ¼²¢½ā“š£Ø±£Įō»Ķ¼ŗŪ¼££©£ŗ
£Ø1£©»³ö”÷A”äB”äC”䣻
£Ø2£©»³ö”÷ABCµÄøߣ¬¼“Ļ߶ĪBD£»
£Ø3£©Į¬½ÓAA”䔢 CC”䣬ÄĒĆ“AA”äÓėCC”äµÄ¹ŲĻµŹĒ________£»Ļ߶ĪACÉعżĶ¼ŠĪµÄĆ껿ĪŖ____£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻßy=a1£Øx©2£©2+2Óėy=a2£Øx©2£©2©3µÄ¶„µć·Ö±šĪŖA£¬B£¬ÓėxÖį·Ö±š½»ÓŚµćO£¬C£¬D£¬E£®ČōµćDµÄ×ų±źĪŖ£Ø©1£¬0£©£¬Ōņ”÷ADEÓė”÷BOCµÄĆ껿±ČĪŖ £® 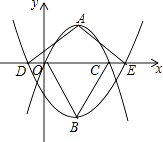
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćPĪŖ”÷ABCµÄÄŚŠÄ£¬ŃÓ³¤AP½»”÷ABCµÄĶā½ÓŌ²ÓŚD£¬ŌŚACŃÓ³¤ĻßÉĻÓŠŅ»µćE£¬Āś×ćAD2=ABAE£®
ĒóÖ¤£ŗDEŹĒ”ŃOµÄĒŠĻߣ®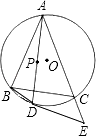
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬³¤·½ŠĪ![]() ·ÅÖĆŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖµć
·ÅÖĆŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖµć![]() £¬µć
£¬µć![]() £¬¶Æµć
£¬¶Æµć![]() “Ó
“Ó![]() ³ö·¢£¬ŃŲ
³ö·¢£¬ŃŲ![]() ŅŌĆæĆė
ŅŌĆæĆė![]() øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æ£¬Ķ¬Ź±£¬¶Æµć
øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æ£¬Ķ¬Ź±£¬¶Æµć![]() “Ó
“Ó![]() ³ö·¢£¬ŃŲ
³ö·¢£¬ŃŲ![]() ŅŌĆæĆė
ŅŌĆæĆė![]() øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æ£®µ±ĘäÖŠŅ»µćµ½“ļ
øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æ£®µ±ĘäÖŠŅ»µćµ½“ļ![]() µćŹ±£¬Į½¶ÆµćĶ¬Ź±Ķ£Ö¹ŌĖ¶ÆÉčŌĖ¶ÆŹ±¼äĪŖ
µćŹ±£¬Į½¶ÆµćĶ¬Ź±Ķ£Ö¹ŌĖ¶ÆÉčŌĖ¶ÆŹ±¼äĪŖ![]() £®
£®

£Ø1£©µ±![]() ______Ź±£¬µć
______Ź±£¬µć![]() ×·ÉĻµć
×·ÉĻµć![]() £¬“ĖŹ±µć
£¬“ĖŹ±µć![]() µÄ×ų±źĪŖ_______£®
µÄ×ų±źĪŖ_______£®
£Ø2£©µ±![]() Ź±£¬·Ö±šČ”
Ź±£¬·Ö±šČ”![]() ”¢
”¢![]() µÄÖŠµć
µÄÖŠµć![]() ”¢
”¢![]() £¬Čē¹ūĖıߊĪ
£¬Čē¹ūĖıߊĪ![]() µÄĆ껿µČÓŚ
µÄĆ껿µČÓŚ![]() £¬ĒėĒó³öŹ±¼ä
£¬ĒėĒó³öŹ±¼ä![]() µÄȔֵ£»
µÄȔֵ£»
£Ø3£©ČēĶ¼2£¬Į¬½Ó![]() £¬ŅŃÖŖ
£¬ŅŃÖŖ![]() £¬ŌŚ£Ø2£©ĪŹµÄĢõ¼žĻĀ£¬¹żµć
£¬ŌŚ£Ø2£©ĪŹµÄĢõ¼žĻĀ£¬¹żµć![]() ×÷
×÷![]() ÓŚµć
ÓŚµć![]() £¬ĪŹŌŚ³¤·½ŠĪ
£¬ĪŹŌŚ³¤·½ŠĪ![]() µÄĖÄĢõ±ßÉĻŹĒ·ń“ęŌŚµć
µÄĖÄĢõ±ßÉĻŹĒ·ń“ęŌŚµć![]() £¬Ź¹µĆĻ߶Ī
£¬Ź¹µĆĻ߶Ī![]() £¬Čō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµć
£¬Čō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµć![]() µÄ×ų±ź£¬Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄ×ų±ź£¬Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDŹĒĘ½ŠŠĖıߊĪ£¬PŹĒCDÉĻŅ»µć£¬ĒŅAPŗĶBP·Ö±šĘ½·Ö”ĻDABŗĶ”ĻCBA.

(1)Ēó”ĻAPBµÄ¶ČŹż£»
(2)Čē¹ūAD£½5 cm£¬AP£½8 cm£¬Ēó”÷APBµÄÖܳ¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻABC=90”ć£¬AB=BC£¬µćAŌŚxÖįµÄøŗ°ėÖįÉĻ£¬µćBŹĒyÖįÉĻµÄŅ»øö¶Æµć£¬µćCŌŚµćBµÄÉĻ·½£¬
£Ø1£©ČēĶ¼1µ±µćAµÄ×ų±źĪŖ£Ø©3£¬0£©£¬µćBµÄ×ų±źĪŖ£Ø0£¬1£©Ź±£¬ĒóµćCµÄ×ų±ź£»
£Ø2£©ÉčµćAµÄ×ų±źĪŖ£Øa£¬0£©£¬µćBµÄ×ų±źĪŖ£Ø0£¬b£©£®¹żµćC×÷CD”ĶyÖįÓŚµćD£¬ŌŚµćBŌĖ¶Æ¹ż³ĢÖŠ£Ø²»°üŗ¬”÷ABCµÄŅ»±ßÓė×ų±źÖįÖŲŗĻµÄĒéæö£©£¬²ĀĻėĻ߶ĪODµÄ³¤Óėa”¢bµÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀČēĶ¼4£¬µ±xÖįĘ½·Ö”ĻBACŹ±£¬BC½»xÖįÓŚµćE£¬¹żµć×÷CF”ĶxÖįÓŚµćF£®ĖµĆ÷“ĖŹ±Ļ߶ĪCFÓėAEµÄŹżĮæ¹ŲĻµ£ØÓĆŗ¬a”¢bµÄŹ½×Ó±ķŹ¾£©£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”ææģµŻ¹«Ė¾×¼±ø¹ŗĀņ»śĘ÷ČĖĄ““śĢęČĖ¹¤·Ö¼šŅŃÖŖ¹ŗĀņ- Ģؼ׊Ķ»śĘ÷ČĖ±Č¹ŗĀņ-ĢØŅŅŠĶ»śĘ÷ČĖ¶ą![]() ĶņŌŖ£»¹ŗĀņ
ĶņŌŖ£»¹ŗĀņ![]() Ģؼ׊Ķ»śĘ÷ČĖŗĶ
Ģؼ׊Ķ»śĘ÷ČĖŗĶ![]() ĢØŅŅŠĶ»śĘ÷ČĖ¹²Šč
ĢØŅŅŠĶ»śĘ÷ČĖ¹²Šč![]() ĶņŌŖ.
ĶņŌŖ.
(1)Ēó¼×”¢ŅŅĮ½ÖÖŠĶŗŵĻśĘ÷ČĖĆæĢصļŪøńø÷ŹĒ¶ąÉŁĶņŌŖ£»
(2)ŅŃÖŖ¼×ŠĶ”¢ŅŅŠĶ»śĘ÷ČĖĆæĢØĆ抔Ź±·Ö¼šæģµŻ·Ö±šŹĒ![]() ¼ž”¢
¼ž”¢![]() ¼ž£¬øĆ¹«Ė¾¼Ę»®×ī¶ąÓĆ
¼ž£¬øĆ¹«Ė¾¼Ę»®×ī¶ąÓĆ![]() ĶņŌŖ¹ŗĀņ
ĶņŌŖ¹ŗĀņ![]() ĢØÕāĮ½ÖÖŠĶŗŵĻśĘ÷ČĖ.øĆ¹«Ė¾øĆČēŗĪ¹ŗĀņ£¬²ÅÄÜŹ¹µĆĆ抔Ź±µÄ·Ö¼šĮæ×ī“ó£æ
ĢØÕāĮ½ÖÖŠĶŗŵĻśĘ÷ČĖ.øĆ¹«Ė¾øĆČēŗĪ¹ŗĀņ£¬²ÅÄÜŹ¹µĆĆ抔Ź±µÄ·Ö¼šĮæ×ī“ó£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com