
 在平面直角坐标系xOy中,A(t,0),B(t+$\sqrt{3}$,0),对于线段AB和x轴上方的点P给出如下定义:当∠APB=60°时,称点P为AB的“等角点”.
在平面直角坐标系xOy中,A(t,0),B(t+$\sqrt{3}$,0),对于线段AB和x轴上方的点P给出如下定义:当∠APB=60°时,称点P为AB的“等角点”.分析 (1)根据给定的t值找出A、B点的坐标,再利用解三角形的方法讨论C、D、E点是否满足“等角点”的条件即可得出结论;
(2)①画出点N在y轴正半轴时图形,通过角的计算得出∠PAB=∠OMN,从而得出“PA=PM,AB=BM”,再通过解直角三角形即可得出P点的坐标,同理可得出点N在y轴负半轴时的P点的坐标;②通过角的计算找出∠BMQ=∠MQB=30°,再结合外角的性质得出BQ=BM=AB即得出△ABQ是等边三角形,从而得出结论,同理点N在y轴负半轴时,结论相同;
(3)通过构建与y轴以及与线段MN相切的圆,找出点A与点B的临界点,求出此时的t值,从而得出线段AB的所有“等角点”都在△MON内部,则t的取值范围.
解答 解:(1)当t=-$\frac{\sqrt{3}}{2}$时,点A(-$\frac{\sqrt{3}}{2}$,0),点B($\frac{\sqrt{3}}{2}$,0),
∵点C(0,$\frac{3}{2}$),OC=$\frac{3}{2}$=$\frac{\sqrt{3}}{2}$AB,且点O为线段AB的中点,
∴△ABC为等边三角形,
∴∠ACB=60°,点C是线段AB的“等角点”;
∵点D($\frac{\sqrt{3}}{2}$,1),B、D横坐标相等,
∴BD⊥x轴于点B.
∵AB=$\frac{\sqrt{3}}{2}$-(-$\frac{\sqrt{3}}{2}$)=$\sqrt{3}$,BD=1-0=1,tan∠ADB=$\frac{AB}{BD}$=$\sqrt{3}$,
∴∠ADB=60°,点D是线段AB的“等角点”;
∵点E(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$),A、E横坐标相等,
∴AE⊥x轴于点A.
∵AB=$\frac{\sqrt{3}}{2}$-(-$\frac{\sqrt{3}}{2}$)=$\sqrt{3}$,AE=$\frac{3}{2}$-0=$\frac{3}{2}$,tan∠AEB=$\frac{AB}{AE}$=$\frac{2\sqrt{3}}{3}$,
∴∠AEB≠60°,点E不是线段AB的“等角点”.
综上可知:点C、D是线段AB的“等角点”.
故答案为:C、D.
(2)①当点N在y轴正半轴时,如图1,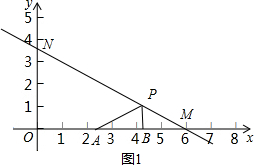
∵∠APB=60°,∠ABP=90°,
∴∠PAB=30°,
又∵∠OMN=30°,
∴PA=PM,AB=BM.
∵AB=$\sqrt{3}$,
∴BM=$\sqrt{3}$,
∴PB=1.
∴P(6-$\sqrt{3}$,1).
当点N在y轴负半轴时,同理可得点P(6+$\sqrt{3}$,1).
②当点N在y轴正半轴时,如图2,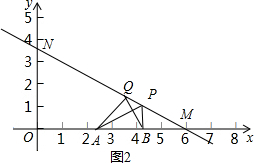
∵BQ⊥AP,且∠APB=60°,
∴∠PBQ=30°,
∴∠ABQ=60°,
∴∠BMQ=∠MQB=30°,
∴BQ=BM=AB,
∴△ABQ是等边三角形.
∴∠AQB=60°.
当点N在y轴负半轴时,同理可得∠AQB=90°.
③以AB=$\sqrt{3}$做底,AO′=BO′为腰,∠AO′B=120°作三角形,如图3所示.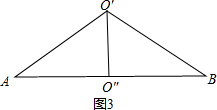
∵AO′=BO′,AB=$\sqrt{3}$,∠AO′B=120°,
∴AO′=1,O′O″=$\frac{1}{2}$.
(i)在(2)的基础上,以直线y=$\frac{1}{2}$上的点O′为圆心,1为半径作圆,当圆O′与y轴相切,且O′在y轴右侧时,如图4所示,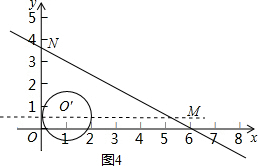
此时O′的坐标为(1,$\frac{1}{2}$),此时A点的横坐标为1-$\frac{1}{2}$AB=1-$\frac{\sqrt{3}}{2}$,
即t=1-$\frac{\sqrt{3}}{2}$;
(ii)在(2)的基础上,以直线y=$\frac{1}{2}$上的点O′为圆心,1为半径作圆,当圆O′与线段MN相切,且O′在MN下方时,如图5所示.
∵M′F=$\frac{1}{2}$,∠OMN=30°,
∴MF=$\frac{M′F}{tan∠OMN}$=$\frac{\sqrt{3}}{2}$.
∵O′D=1,∠O′M′D=∠OMN=30°,
∴O′M′=$\frac{O′D}{sin∠O′M′D}$=2.
此时点B的横坐标为OM-MF-O′M′+$\frac{1}{2}$AB=4,
∴t+$\sqrt{3}$=4,t=4-$\sqrt{3}$.
综上可知:若线段AB的所有“等角点”都在△MON内部,则t的取值范围是1-$\frac{\sqrt{3}}{2}$<t<4-$\sqrt{3}$.
故答案为:1-$\frac{\sqrt{3}}{2}$<t<4-$\sqrt{3}$.
点评 本题考查了一次函数的综合应用、角的计算、解直角三角形、切线的性质以及等腰(等边)三角形的性质,解题的关键:(1)通过三角形的计算找出角的值;(2)①通过解直角三角形求出点P的坐标;②找出△ABQ是等边三角形;③通过相切寻找临界点.本题属于中档题,(1)(2)难度不大,(2)中③难度不小,在寻找A、B点的过程中,通过构建满足条件的圆,来寻找临界点,解题过程不难,但是点的寻找比较困难,此处与切线的性质练习较大,在日常练习中应加强训练.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
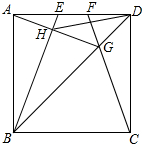 如图,E、F是正方形ABCD的边AD上有两个动点,满足AE=DF,连接CF交BD于G,连接BE交AG于点H,若正方形的边长为3,则线段DH长度的最小值是$\frac{3}{2}$($\sqrt{5}$-1).
如图,E、F是正方形ABCD的边AD上有两个动点,满足AE=DF,连接CF交BD于G,连接BE交AG于点H,若正方形的边长为3,则线段DH长度的最小值是$\frac{3}{2}$($\sqrt{5}$-1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
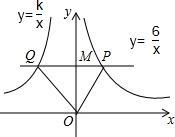 如图,在平面直角坐标系中,过点M(0,2)的直线与x轴平行,且直线分别于函数y=$\frac{6}{x}$(x>0)和y=$\frac{k}{x}$(x<0)的图象交于点P、Q,若△POQ的面积为8,则k的值为-10.
如图,在平面直角坐标系中,过点M(0,2)的直线与x轴平行,且直线分别于函数y=$\frac{6}{x}$(x>0)和y=$\frac{k}{x}$(x<0)的图象交于点P、Q,若△POQ的面积为8,则k的值为-10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
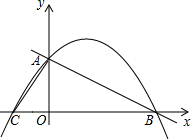 如图,在直角坐标系中,已知直线y=-$\frac{1}{2}$x+4与y轴交于A点,与x轴交于B点,C点的坐标为(-2,0).
如图,在直角坐标系中,已知直线y=-$\frac{1}{2}$x+4与y轴交于A点,与x轴交于B点,C点的坐标为(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:在△ABC中,AB=AC.
已知:在△ABC中,AB=AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com