
����Ŀ����ͼ���ڳ�����ABCD�У�AB=4cm��BC=6cm����EΪAB�е㣬�����P���߶�BC����ÿ��2cm���ٶ��ɵ�B���C�˶���ͬʱ����Q���߶�CD���ɵ�C���D�˶������˶�ʱ��Ϊt��.
(1)��t=2ʱ�����EBP�����
(2)����Q�����P��ͬ���ٶ��˶�������������BPE����CQPȫ�ȣ���ʱ��Q���ٶ��Ƕ��٣�
(3)����Q��(2)�е��˶��ٶȴӵ�C��������P��ԭ�����˶��ٶȴӵ�Bͬʱ����������ʱ���س�����ABCD���ı��˶������ʱ���P���Q��һ���ڳ�����ABCD����������������

���𰸡���1��4cm2����2������1.5���BPE���CQPȫ�ȣ���ʱ��Q���ٶ���![]() cm/s��3������9���P���Q��һ����AB��������.
cm/s��3������9���P���Q��һ����AB��������.
��������
��EBP���������![]() EB��BP��ã���t��EP BP��ʾ������;
EB��BP��ã���t��EP BP��ʾ������;
��2����� Q ���˶��ٶ�Ϊx cm/s���ȸ���ʱ�䡢�ٶȱ�ʾ·��: BP=2t��CP=6-2t��![]() �����ݵ�EΪAB�е��ʾEB=2��������BPE����CPQȫ�ȣ�������������ֱ���ݶ�Ӧ����ȣ��з��̿ɵý��ۣ�
�����ݵ�EΪAB�е��ʾEB=2��������BPE����CPQȫ�ȣ�������������ֱ���ݶ�Ӧ����ȣ��з��̿ɵý��ۣ�
��3����t��ʾ����P�͵�Q��·�̣�������ȣ����t��ֵ���ٸ��������ж��Ƿ�Ϊ��һ������.
�⣺��1����t=2
��BP=2t=4
��E��AB���е㣬AB=4
��EB=2
��S��EBP=![]() EB��BP=4cm2
EB��BP=4cm2
��2����� Q ���˶��ٶ�Ϊx cm/s���� BP=2t��CP=6-2t��![]()
�ߡ�B=��C=90��
�ٵ�BP=CP��BE=CQʱ����BPE�ա�CPQ
��![]()
��ã�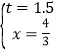
�ڵ�BP=CQ��BE=CPʱ����BPE�ա�CQP
��![]()
��ã�![]()
��x��2
����ȥ�������
��������������1.5����BPE����CQPȫ�ȣ���ʱ��Q���ٶ���![]() cm/s
cm/s
��3��������ã�2t=![]() t+6
t+6
��ã�t=9
��t=9ʱ����P����2��9=18cm
�� 18-BC-CD-AD=2
�� ����9���P���Q��һ����AB��������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���꼶��ѧ��ȤС�������������AB�ĸ߶ȣ�������C�����������ﶥ�ˣ��������Ϊ48�㣬����������ķ���ǰ��6����D�����������Ϊ64�㣬������ĸ߶ȣ���������ĸ߶Ⱥ��Բ��ƣ������ȷ��0.1�ף�
���ο����ݣ�sin48��� ![]() ��tan48���
��tan48��� ![]() ��sin64���
��sin64��� ![]() ��tan64���2��
��tan64���2��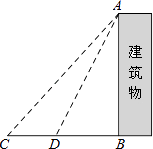
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��5��a��0����x�ύ�ڵ�A����5��0���͵�B��3��0������y�ύ�ڵ�C��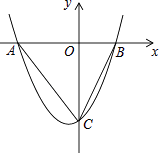
��1����������ߵĽ���ʽ��
��2������EΪx���·��������ϵ�һ���㣬��S��ABE=S��ABCʱ�����E�����ꣻ
��3���ڣ�2���������£����������Ƿ���ڵ�P��ʹ��BAP=��CAE�������ڣ������P�ĺ����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
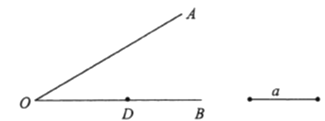
����Ŀ����ͼ����֪![]() Ϊ
Ϊ![]() �ϵ�һ����������Ҫ�������ͼ��
�ϵ�һ����������Ҫ�������ͼ��
��1����![]() ��ƽ����
��ƽ����![]() .
.
��2����![]() ��ȡһ��
��ȡһ��![]() ��ʹ��
��ʹ��![]() .
.
��3�������Խ��С�վ�����ϸ�۲�����������²������ڱ�![]() ��ȡһ��
��ȡһ��![]() ��ʹ��
��ʹ��![]() ����ʱ������
����ʱ������![]() ��
��![]() ֮�����һ����������ϵ����д��
֮�����һ����������ϵ����д��![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��ֱ��������ABCֽƬ��б��AB�ϵ�����CD�������õ���ACD���ٽ���ACD��DB����ƽ�Ƶ���A��C��D���λ�ã���ƽ�ƿ�ʼ���D��δ�����Bʱ��A��C�佻CD��E��D��C�佻CB�ڵ�F������EF�����ı���EDD��FΪ����ʱ����̽����A��DE����״�����жϡ�A��DE���EFC���Ƿ�ȫ�ȣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CΪ�߶�AE��һ���㣨����A��E�غϣ�����AEͬ��ֱ����ȱߡ�ABC�͵ȱߡ�CDE��AD��BE���ڵ�O��AD��BC���ڵ�P��BE��CD���ڵ�Q������PQ������������ۣ���AD=BE����PQ��AE����CP=CQ����BO=OE���ݡ�AOB=60����������Ľ�����
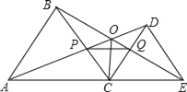
A. �٢ۢ� B. �٢ۢܢ� C. �٢ڢۢ� D. �٢ڢۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���x2+2x��2m+1=0����ʵ����֮��Ϊ������ʵ��m��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���ABCD�У���A=90�㣬AB=3��AD=4��BC=12��CD=13�����ı���ABCD�����.
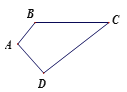
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ABC=90�㣬��M��AC���е㣬��ABΪֱ������O�ֱ�AC��BM�ڵ�D��E��
��1����֤��MD=ME��
��2����գ�
����AB=6����AD=2DMʱ��DE=��
������OD��OE������A�Ķ���Ϊʱ���ı���ODME�����Σ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com