
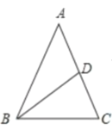
【题目】(1)等腰三角形底边长为6cm,一腰上的中线把它的周长分成两部分的差为2cm,则腰长为________.
(2)已知![]() 的周长为24,
的周长为24,![]() ,
,![]() 于点D,若
于点D,若![]() 的周长为20,则AD的长为________.
的周长为20,则AD的长为________.
(3)已知等腰三角形的周长为24,腰长为x,则x的取值范围是________.
【答案】4cm或8cm 8 ![]()
【解析】
(1)根据题意画出图形,由题意得![]() ,即可得
,即可得![]() ,又由等腰三角形的底边长为6cm,即可求得答案.
,又由等腰三角形的底边长为6cm,即可求得答案.
(2)由△ABC的周长为24得到AB,BC的关系,由△ABD的周长为20得到AB,BD,AD的关系,再由等腰三角形的性质知,BC为BD的2倍,故可解出AD的值.
(3)设底边长为y,再由三角形的三边关系即可得出答案.
(1)如图,![]() ,BD是中线
,BD是中线
由题意得存在两种情况:①![]() ②
②![]()
①![]() ,
,![]()
∵![]()
∴![]()
②![]() ,
,![]()
∵![]()
∴![]()
∴腰长为:4cm或8cm
故答案为:4cm或8cm.
(2)∵△ABC的周长为24,![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]() 的周长为20
的周长为20
∴![]()
∴![]()
故答案为:8.
(3)设底边长为y
∵等腰三角形的周长为24,腰长为x
∴![]()
∴![]() ,即
,即![]()
解得![]()
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数和等于0?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
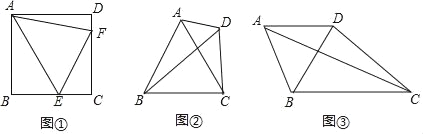
(1)如图①,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,则线段BE、EF、FD之间的数量关系为 ;
(2)如图②,在△ADC中,AD=2,CD=4,∠ADC是一个不固定的角,以AC为边向△ADC的另一侧作等边△ABC,连接BD,则BD的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由;
问题解决
(3)如图③,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4![]() ,若BD⊥CD,垂足为点D,则对角线AC的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由.
,若BD⊥CD,垂足为点D,则对角线AC的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知![]() ,点P在OA上,且
,点P在OA上,且![]() ,点P关于直线OB的对称点是Q,则
,点P关于直线OB的对称点是Q,则![]() ________.
________.
(2)已知![]() ,点P在
,点P在![]() 的内部,
的内部,![]() ,点
,点![]() 和点P关于OA对称,点
和点P关于OA对称,点![]() 和点P关于OB对称,则
和点P关于OB对称,则![]() 、O、
、O、![]() 三点构成的三角形是________三角形,其周长为________.
三点构成的三角形是________三角形,其周长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
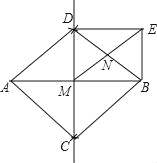
【题目】如图,分别以线段AB两端点A,B为圆心,以大于![]() AB长为半径画弧,两弧交于C,D两点,作直线CD交AB于点M,DE∥AB,BE∥CD.
AB长为半径画弧,两弧交于C,D两点,作直线CD交AB于点M,DE∥AB,BE∥CD.
(1)判断四边形ACBD的形状,并说明理由;
(2)求证:ME=AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“若矩形的两边长分别为3和4,求矩形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若矩形的周长为14,且一边长为3,求另一边的长”;也可以是“若矩形的周长为14,求矩形面积的最大值”,等等.
(1)设A=![]() ,B=
,B=![]() ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为![]() 、
、![]() ,点D是OA的中点,点P在BC边上运动,当
,点D是OA的中点,点P在BC边上运动,当![]() 是等腰三角形时,点Р的坐标为_______________.
是等腰三角形时,点Р的坐标为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
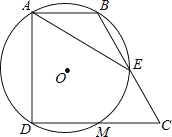
【题目】如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,且CE=1,下列结论:①DM=CM;②![]() ;③⊙O的直径为2;④AE=AD.其中正确的结论有_____(填序号).
;③⊙O的直径为2;④AE=AD.其中正确的结论有_____(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com