
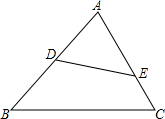
 如图,已知D、E分别在△ABC的边AB、AC上,D为AB的中点,AE:EC=2:1,△ADE∽△ACB,且∠ADE=∠C,求$\frac{DE}{BC}$的值.
如图,已知D、E分别在△ABC的边AB、AC上,D为AB的中点,AE:EC=2:1,△ADE∽△ACB,且∠ADE=∠C,求$\frac{DE}{BC}$的值. 分析 设AE=2x,EC=x,AD=BD=y,根据相似得出比例式,即可求出y=$\sqrt{3}$x,即可求出答案.
解答 解:∵AE:EC=2:1
∴设AE=2x,EC=x,则AC=3x,
∵D为AB中点,
∴AD=BD,
设AD=BD=y,则AB=2y,
∵△ADE∽△ACB,
∴$\frac{AD}{AC}=\frac{DE}{BC}=\frac{AE}{AB}$,
∴$\frac{y}{3x}$=$\frac{DE}{BC}$=$\frac{2x}{2y}$,
∴2y2=6x2,
∴y=$\sqrt{3}$x
∴$\frac{DE}{BC}$=$\frac{y}{3x}$=$\frac{\sqrt{3}x}{3x}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了相似三角形的性质的应用,能求出y=$\sqrt{3}$x是解此题的关键,难度适中.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | ±2 | B. | $\sqrt{2}$ | C. | ±$\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
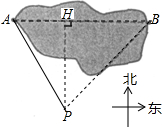 在一次测量活动中,同学们要测量某公园湖的码头A与它正东方向的亭子B之间的距离,如图.他们选择了与码头A、亭子B在同一水平面上的点P,在点P处测得码头A位于点P北偏西30°方向,亭子B位于点P北偏东43°方向;又测得点P与码头A之间的距离为400米.请你运用以上测得的数据求出码头A与亭子B之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.7,tan43°≈0.93,sin43°≈0.68.)
在一次测量活动中,同学们要测量某公园湖的码头A与它正东方向的亭子B之间的距离,如图.他们选择了与码头A、亭子B在同一水平面上的点P,在点P处测得码头A位于点P北偏西30°方向,亭子B位于点P北偏东43°方向;又测得点P与码头A之间的距离为400米.请你运用以上测得的数据求出码头A与亭子B之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.7,tan43°≈0.93,sin43°≈0.68.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
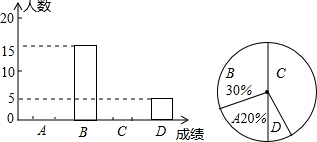 某校九年级一模考试,数学老师为了了解学生的学习情况,随机抽取50名学生的数学成绩进行统计分析,得出相关统计表和统计图如下:
某校九年级一模考试,数学老师为了了解学生的学习情况,随机抽取50名学生的数学成绩进行统计分析,得出相关统计表和统计图如下:| 成绩/分 | 111~120 | 101~110 | 91~100 | 90及90以下 |
| 成绩等级 | A | B | C | D |
| 人数 | m | 15 | n | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
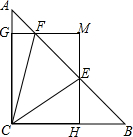 如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正确结论为( )
如图,在△ABC中,∠ACB=90°,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=$\sqrt{2}$;②当点E与点B重合时,MH=$\frac{1}{2}$;③AF+BE=EF;④MG•MH=$\frac{1}{2}$,其中正确结论为( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
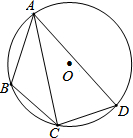 如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是$\frac{8\sqrt{3}}{3}$.
如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是$\frac{8\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为加强公民的节水意识,合理利用水资源.某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于1:1.5:2.如图折线表示实行阶梯水价后每月水费y(元)与用水量xm3之间的函数关系.其中线段AB表示第二级阶梯时y与x之间的函数关系
为加强公民的节水意识,合理利用水资源.某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于1:1.5:2.如图折线表示实行阶梯水价后每月水费y(元)与用水量xm3之间的函数关系.其中线段AB表示第二级阶梯时y与x之间的函数关系查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com