
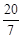 或﹣3+
或﹣3+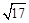 ;
;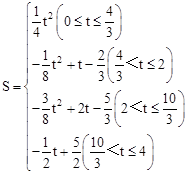 .
.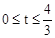 ,
,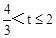 ,
,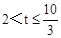 和
和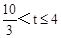 时去分析求解即可求得答案:
时去分析求解即可求得答案: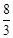 .
.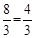 .
. t,∴FM=
t,∴FM= t,
t,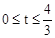 时,S=S△FMN=
时,S=S△FMN= ×t×
×t× t=
t=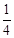 t2.
t2.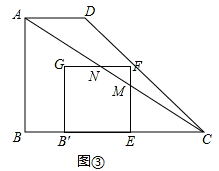
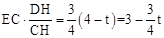 ,∴FK=2﹣EK=
,∴FK=2﹣EK=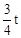 ﹣1.
﹣1.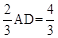 ,∴FL=t﹣
,∴FL=t﹣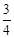 ,∴当
,∴当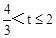 时,S=S△FMN﹣S△FKL=
时,S=S△FMN﹣S△FKL=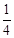 t2﹣
t2﹣ (t﹣
(t﹣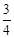 )(
)(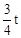 ﹣1)=
﹣1)=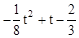 .
.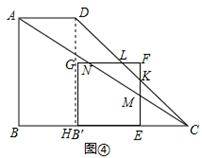
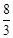 ,
,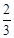 . ∴t=
. ∴t=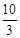 .
. B′C=
B′C= (6﹣t)=3﹣
(6﹣t)=3﹣ t,∴GN=GB′﹣B′N=
t,∴GN=GB′﹣B′N= t﹣1.
t﹣1.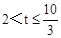 时,S=S梯形GNMF﹣S△FKL=
时,S=S梯形GNMF﹣S△FKL= ×2×(
×2×( t﹣1+
t﹣1+ t)﹣
t)﹣ (t﹣
(t﹣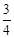 )(
)(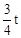 ﹣1)=
﹣1)=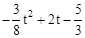 .
.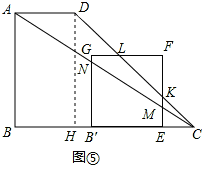
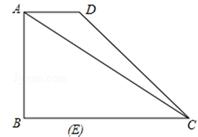
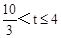 时,
时,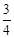 B′C=
B′C=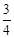 (6﹣t),EK=
(6﹣t),EK=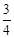 EC=
EC=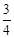 (4﹣t),B′N=
(4﹣t),B′N= B′C=
B′C= (6﹣t)EM=
(6﹣t)EM= EC=
EC= (4﹣t),
(4﹣t),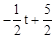 .
.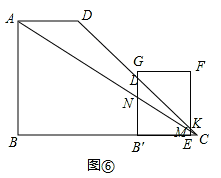
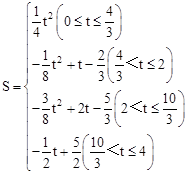 .
.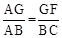 ,即
,即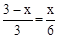 ,解得:x=2,即BE=2.
,解得:x=2,即BE=2.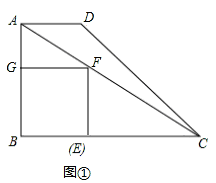
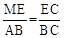 ,即
,即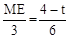 . ∴ME=2﹣
. ∴ME=2﹣ t.
t. t)2=
t)2=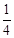 t2﹣2t+8.
t2﹣2t+8. t,∴DN=DH﹣NH=3﹣(2﹣
t,∴DN=DH﹣NH=3﹣(2﹣ t)=
t)= t+1.
t+1. t+1)2+ t 2=
t+1)2+ t 2=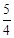 t2+t+1.
t2+t+1.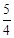 t2+t+1=(
t2+t+1=(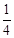 t2﹣2t+8)+(t2﹣4t+13),解得:t=
t2﹣2t+8)+(t2﹣4t+13),解得:t=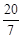 .
.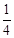 t2﹣2t+8)+(
t2﹣2t+8)+(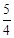 t2+t+1),解得:t1=﹣3+
t2+t+1),解得:t1=﹣3+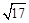 ,t2=﹣3﹣
,t2=﹣3﹣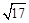 (舍去).∴t=﹣3+
(舍去).∴t=﹣3+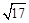 .
.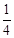 t2﹣2t+8=(t2﹣4t+13)+(
t2﹣2t+8=(t2﹣4t+13)+(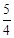 t2+t+1),此方程无解.
t2+t+1),此方程无解.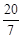 或﹣3+
或﹣3+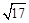 时,△B′DM是直角三角形.
时,△B′DM是直角三角形.
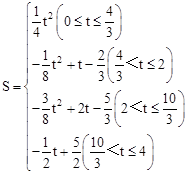 .
.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:计算题


 =DM·EN
=DM·EN查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.10米 | B.12米 | C.15米 | D.22.5米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com