练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．计算：（$\sqrt{8}$+$\sqrt{50}$）-（$\sqrt{18}$-$\sqrt{\frac{1}{8}}$）

    分析 首先化简二次根式，进而合并求出答案．

    解答 解：原式=（2$\sqrt{2}$+5$\sqrt{2}$）-（3$\sqrt{2}$-$\frac{\sqrt{2}}{4}$）
    =7$\sqrt{2}$-3$\sqrt{2}$+$\frac{\sqrt{2}}{4}$
    =$\frac{17\sqrt{2}}{4}$．

    点评 此题主要考查了二次根式的加减运算，正确化简二次根式是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    17．在代数式$\frac{1}{2}$x2-3x，$\frac{2{x}^{2}y}{π}$，$\frac{1}{x}$，-6，a，0中，单项式有4个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．老师在黑板上出了一道解方程的题$\frac{2x-1}{3}$=1-$\frac{x+2}{4}$，小明马上举起了手，要求到黑板上去做，
    他是这样做的：

    老师说小明解一元一次方程的一般步骤都掌握了，但解题时有一步做错了，请你指出他错在第①步；（填编号）
    然后，请你解方程：$\frac{2x-1}{3}$=1-$\frac{x+2}{4}$相信你，一定做得对．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．在平面直角坐标系中，点P（m，m）（m＞0）是过原点的直线上的动点．以P为端点在OP两侧作射线，其中射线PA交x轴于点B，交y轴于点A（0，m-a），射线PC交x轴于点C （m+a，0），m＞a＞0．是否存在点P，使得以P，B，C为顶点的三角形与△OAC相似？若存在，求此时tan∠OPC的值；若不存在．请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．代数式x2+6x-8，当x=-3时有最小值是-17．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．使式子$\frac{\sqrt{3-x}}{x}$有意义的实数x的取值范围x≤3，且x≠0．

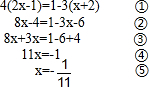
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

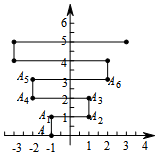    19．如图，在平面直角坐标系上有个点A（-1，0），点A第1次向上跳动一个单位至点A1（-1，1），紧接着第2次向右跳动2个单位至点A2（1，1），第3次向上跳动1个单位，第4次向左跳动3个单位，第5次又向上跳动1个单位，第6次向右跳动4个单位，…，依次规律跳动下去，点A第2015次跳动至点A2015的坐标是（　　）
    A．（504，1008）B．（-504，1007）C．（503，1007）D．（-503，1008）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

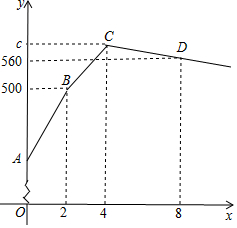    16．某手工编织厂生产一种旅游纪念品，现有60名工人进行手工编织（每人编织的效率相同），2天后抽出10名工人执行其他任务，其余工人继续编织生产；2天后从编织的工人中再抽出10名进行销售（每人每天的销售量相同）．已知每人每天的销售量是编织量的5倍，下图是产品库存量y（件）与生产时间x（天）之间的函数关系图象．
    （1）解释点B的实际意义；
    （2）求每人每天的编织量和销售量；
    （3）求CD段所在的直线的函数表达式，并求出多少天后剩余库存量低于生产前的库存量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图，在平面直角坐标系中，小猫遮住的点的坐标可能是（　　）
    A．（-2，1）B．（2，3）C．（3，-5）D．（-6，-2）

    查看答案和解析>>

    同步练习册答案