
 已知:如图,在?ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
已知:如图,在?ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.分析 (1)先证明△ABE≌△FCE,推出AE=EF,又BE=CE,即可推出四边形ABFC是平行四边形;
(2)根据等底同高三角形面积线段,三角形的中线分成的两个三角形的面积相等,即可判定;
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠ABE=∠FCE,
在△ABE和△FCE中,
$\left\{\begin{array}{l}{∠ABE=∠FCE}\\{BE=CE}\\{∠AEB=∠CEF}\end{array}\right.$
∴△ABE≌△FCE,
∴AE=EF,∵BE=CE,
∴四边形ABFC是平行四边形.
(2)图中与△ABC面积相等的三角形有:△ACF,△BCF,△ABF,△ACD.
点评 本题考查平行四边形的性质和判定、全等三角形的判定和性质等知识,熟练掌握等底同高的三角形的面积相等解决问题,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
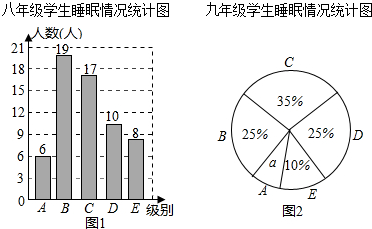
| 组别 | 睡眠时间x |
| A | 4.5≤x<5.5 |
| B | 5.5≤x<6.5 |
| C | 6.5≤x<7.5 |
| D | 7.5≤x<8.5 |
| E | 8.5≤x<9.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为2或1.
如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为2或1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知l1∥l2,直角三角板的直角顶点在直线l2上,若∠1=58°,则下列结论错误的是( )
如图,已知l1∥l2,直角三角板的直角顶点在直线l2上,若∠1=58°,则下列结论错误的是( )| A. | ∠3=58° | B. | ∠4=122° | C. | ∠5=52° | D. | ∠2=58° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明、小华利用五一假期结伴游览某旅游景点,她们想测量景点内一条小河的宽度,如图,已知观测点C距离地面高度CH=40m,她们测得正前方河两岸A、B两点处的俯角分别为45°和30°,请计算出该处的河宽AB约为多少米?(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
小明、小华利用五一假期结伴游览某旅游景点,她们想测量景点内一条小河的宽度,如图,已知观测点C距离地面高度CH=40m,她们测得正前方河两岸A、B两点处的俯角分别为45°和30°,请计算出该处的河宽AB约为多少米?(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com