
【题目】如图,一个质地均匀的正四面体的四个面上依次标有数字-2,0,1,2,连续抛掷两次,朝下一面的数字分别是a,b,将其作为M点的横、纵坐标,则点M(a,b)落在以A(6,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的概率是________.
【答案】![]()
【解析】
首先列举出所有可能的结果,再找出落在以A(6,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的可能情况,再根据概率公式得到结果即可.
解:列表如下:
b | -2 | 0 | 1 | 2 |
-2 | (-2,-2) | (-2,0) | (-2,1) | (-2,2) |
0 | (0,-2) | (0,0) | (0,1) | (0,2) |
1 | (1,-2) | (1,0) | (1,1) | (1,2) |
2 | (2,-2) | (2,0) | (2,1) | (2,2) |
共有16种结果,而落在以A(6,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)有:(0,2),(1,1),(2,0),(2,1)共4种可能情况,如图:
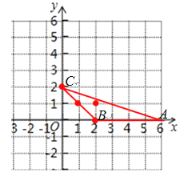
所以落在以A(6,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的概率是:![]() ,
,
故答案为:![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】重庆是长江上游地区的经济中心、金融中心和创新中心.某公司为了调动员工积极性,将公司员工分成了三个小组进行集分制考核:每月销售业绩第一名集x分,销售业绩第二名集y分,销售业绩第三名集0分(x>y,且均为正整数),经过若干个月(超过4个月)考核后,第一小组集分为23分,第二小组集分为20分,第三小组集分为9分,则第一小组最多得到_____次第二名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“武汉加油!中国加油!”疫情牵动万人心,每个人都在为抗击疫情而努力.某厂改造了![]() 条口罩生产线,每条生产线每天可生产口罩
条口罩生产线,每条生产线每天可生产口罩![]() 个.如果每增加一条生产线,每条生产线就会比原来少生产
个.如果每增加一条生产线,每条生产线就会比原来少生产![]() 个口罩.设增加
个口罩.设增加![]() 条生产线后,每条生产线每天可生产口罩
条生产线后,每条生产线每天可生产口罩![]() 个.
个.
![]() 直接写出
直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 若每天共生产口罩
若每天共生产口罩![]() 个,在投入人力物力尽可能少的情况下,应该增加几条生产线?
个,在投入人力物力尽可能少的情况下,应该增加几条生产线?
![]() 设该厂每天可以生产的口罩
设该厂每天可以生产的口罩![]() 个,请求出
个,请求出![]() 与
与![]() 的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?
的函数关系式,并求出增加多少条生产线时,每天生产的口罩数量最多,最多为多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
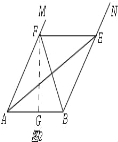
【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DE上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
(1)求sin∠EAC的值.
(2)求线段AH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
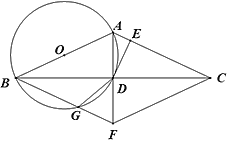
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,DE⊥AC,垂足为E,CF∥AB交AD延长线于点F,连接BF交⊙O于点G,连接DG.
(1)求证:DE为⊙O的切线;
(2)求证:四边形ABFC为菱形;
(3)若OA=5,DG=2![]() ,求线段GF的长.
,求线段GF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成一件事有几类办法,各类办法相互独立,每类办法中又有多种不同的办法,则完成这件事的不同办法数是各类不同方法种数的和,这就是分类计数原理,也叫做加法原理.完成一件事,需要分成几个步骤,每一步的完成有多种不同的方法,则完成这件事的不同方法种数是各种不同的方法数的乘积,这就是分步计数原理,也叫做乘法原理.
小王同学参加某高中学校进行的自主招生考试,本次考试共有1000人参加.
(1)1000人参加自招考试,有300人可以享受加分政策,且有10,20,30,60四个档次,小王想获得至少30分的加分,那么概率为多少?
(2)若该高中的中考录取分数线为530分,小王估得中考分数可能在500-509,510-519,520-529三个分段,
①若小王的中考分数在510~519分段,则小王被该高中录取的概率为多少?
②若小王的中考分数在三个分数段对应的概率分别为![]() ,
,![]() ,
,![]() ,则小王被该高中录取的概率为多少?
,则小王被该高中录取的概率为多少?
加分 | 人数 |
10 | 30 |
20 | 90 |
30 | 150 |
60 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点
中的点![]() ,
,![]() ,给出如下定义:若
,给出如下定义:若![]() ,
,![]() 为某个三角形的顶点,且边
为某个三角形的顶点,且边![]() 上的高
上的高![]() ,满足
,满足![]() ,则称该三角形为点
,则称该三角形为点![]() ,
,![]() 的“生成三角形”.
的“生成三角形”.
(1)已知点![]() ;
;
①若以线段![]() 为底的某等腰三角形恰好是点
为底的某等腰三角形恰好是点![]() ,
,![]() 的“生成三角形”,求该三角形的腰长;
的“生成三角形”,求该三角形的腰长;
②若![]() 是点
是点![]() ,
,![]() 的“生成三角形”,且点
的“生成三角形”,且点![]() 在
在![]() 轴上,点
轴上,点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的坐标为______;
的坐标为______;
(2)![]() 的圆心为点
的圆心为点![]() ,半径为2,点
,半径为2,点![]() 的坐标为
的坐标为![]() ,
,![]() 为直线
为直线![]() 上一点,若存在
上一点,若存在![]() ,是点
,是点![]() ,
,![]() 的“生成三角形”,且边
的“生成三角形”,且边![]() 与
与![]() 有公共点,直接写出点
有公共点,直接写出点![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合).
对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com