
【题目】某校初二对某班最近一次数学测验或续(得分取整数)进行统计分析,将所有成绩由低到高分成五组,并绘制成如图所示的频数分布直方图,请结合直方图提供的信息,回答下列问题:
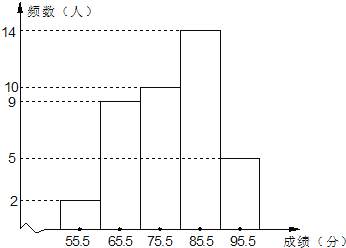
(1)该班共有名同学参加这次测验;
(2)这次测验成绩的中位数落在第几组内(从左到右数);
(3)若该校一共有360名初二学生参加这次测验,成绩80分以上(不含80分)为优秀,估计该校这次数学测验的优秀人数是多少人?
【答案】(1)40名;(2)第三组;(3)171人
【解析】
(1)将五组学生人数加起来即为班级参加测验的学生人数;
(2)将40个数据从小到大排列后,中位数为第20、21位的两个数的平均数,即落在第3组;
(3)用样本估计总体,样本中优秀的占比为![]() ,估计总体中优秀也占
,估计总体中优秀也占![]() ,用360乘
,用360乘![]() 即可解答.
即可解答.
解:(1)2+9+10+14+5=40人,
答:该班共有40名学生参加测验.
(2)40个数据从小到大排列后处在第20、21位的两个数的平均数是中位数,而第20、21位的两个数都落在第3组,
答:这次测验成绩的中位数落在第三组.
(3)360×![]() =171人,
=171人,
答:该校360名学生中这次数学测验为优秀的人数是171人.


科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() 是AC中点,BE平分
是AC中点,BE平分![]() 交AC于点E,点O是AB上一点,
交AC于点E,点O是AB上一点,![]() 过B、E两点,交BD于点G,交AB于点
过B、E两点,交BD于点G,交AB于点![]() ,
,![]() 则下面结论正确的有
则下面结论正确的有![]() 填序号
填序号![]() ______(1)
______(1)![]() 与
与![]() 相切;(2)
相切;(2)![]() ;(3)
;(3)![]() 的直径等于8;(4)
的直径等于8;(4)![]() AE
AE

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、已两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲商场所有商品按![]() 折出售,乙商场对一次购物中超过200元后的价格部分打
折出售,乙商场对一次购物中超过200元后的价格部分打![]() 折. 设原价购物金额累计为
折. 设原价购物金额累计为![]() 元(
元(![]() ).
).
![]() 根据题意,填写下表: (单位:元)
根据题意,填写下表: (单位:元)
原价购物金额累计/元. | 130 | 300 | 700 | ··· |
甲商场实际购物金额/元 | 104 | 560 | ··· | |
乙商场实际购物金额/元 | 130 | 270 | ··· |
![]() 设在甲商场实际购物金额为
设在甲商场实际购物金额为![]() 元,在乙商场实际购物金额为
元,在乙商场实际购物金额为![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
![]() 根据题意填空:
根据题意填空:
①若在同甲商场和在乙商场实际购物花费金额一样多,则在同一商场所购商品原价金额累计为______元 ;
②若在同一商场购物,商品原价购物金额累计为![]() 元,则在甲、乙.两家商场中的 商场实际购物花费金少.
元,则在甲、乙.两家商场中的 商场实际购物花费金少.
③若在同一商场实际购物金额为![]() 元,则在甲、乙两家商场中的_____商场商品原价购物累计金额多.
元,则在甲、乙两家商场中的_____商场商品原价购物累计金额多.
查看答案和解析>>
科目:初中数学 来源: 题型:
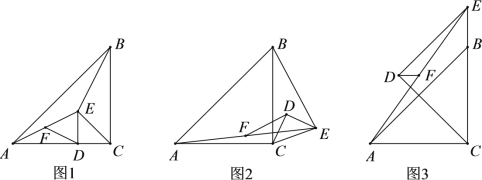
【题目】在△ABC与△CDE中,∠ACB![]() ∠CDE
∠CDE![]() 90°,AC
90°,AC![]() BC,CD
BC,CD![]() ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
ED,连接AE,BE,F为AE的中点,连接DF,△CDE绕着点C旋转.
(1)如图1,当点D落在AC上时,DF与BE的数量关系是: ;
(2)如图2,当△CDE旋转到该位置时,DF与BE是否仍具有(1)中的数量关系,如果具有,请给予证明;如果没有,请说明理由;
(3)如图3,当点E落在线段CB延长线上时,若CD![]() AC
AC![]() 2,求DF的长.
2,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,点A(4,0),点B(0,4),C是AB中点,连接OC,将△AOC绕点A顺时针旋转,得到△AMN,记旋转角为α,点O,C的对应点分别是M,N.连接BM,P是BM中点,连接OP,PN.
(Ⅰ)如图①.当α=45°时,求点M的坐标;
(Ⅱ)如图②,当α=180°时,求证:OP=PN且OP⊥PN;
(Ⅲ)当△AOC旋转至点B,M,N共线时,求点M的坐标(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解,并解答问题:
如图所示的8×8网格都是由边长为1的小正方形组成,图①中的图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.赵爽通过对这种图形切割、拼接,巧妙地利用面积关系证明了著名的勾股定理,它表现了我国古人对数学的钻研精神和聪明才智,是我国数学史上的骄傲.

问题:
请用“赵爽弦图”中的四个直角三角形通过你所学过的图形变化,在图②,图③的方格纸中设计另外两个不同的图案,每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠.画图要求:
(1)图②中所设计的图案(不含方格纸)必须是轴对称图形但不是中心对称图形;
(2)图③中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△EDF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
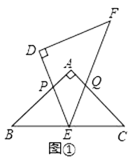
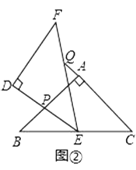
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;
(3)在(2)的条件下,BP=2,CQ=9,则BC的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林家的洗手台面上有一瓶洗手液(如图1),当手按住顶部A下压时(如图2),洗手液瞬间从喷口B流出,已知瓶子上部分的![]() 和
和![]() 的圆心分别为D,C,下部分的视图是矩形CGHD,GH=10cm,GC=8cm,点E到台面GH的距离为14cm,点B距台面GH的距离为16cm,且B,D,H三点共线.如果从喷口B流出的洗手液路线呈抛物线形,且该路线所在的抛物线经过C.E两点,接洗手液时,当手心O距DH的水平距离为2cm时,手心O距水平台面GH的高度为_____cm.
的圆心分别为D,C,下部分的视图是矩形CGHD,GH=10cm,GC=8cm,点E到台面GH的距离为14cm,点B距台面GH的距离为16cm,且B,D,H三点共线.如果从喷口B流出的洗手液路线呈抛物线形,且该路线所在的抛物线经过C.E两点,接洗手液时,当手心O距DH的水平距离为2cm时,手心O距水平台面GH的高度为_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )
①小亮测试成绩的平均数比小明的高;②小亮测试成绩比小明的稳定;③小亮测试成绩的中位数比小明的高;④小亮参加第一轮比赛,小明参加第二轮比赛,比较合理.
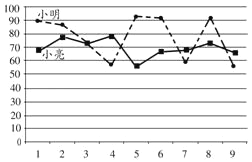
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com