
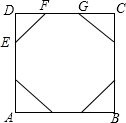
 现有边长为a的正方形花布,问怎样剪裁,才能得到一个面积最大的正八边形花布来做一个形状为正八边形的风筝?
现有边长为a的正方形花布,问怎样剪裁,才能得到一个面积最大的正八边形花布来做一个形状为正八边形的风筝?  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 20、如图,现有边长为a的正方形纸片1张、边长为b的正方形纸片2张,边长分别为a,b的长方形纸片3张,把它们拼成一个长方形.请利用此拼图中的面积关系,分解因式:a2+3ab+2b2=
20、如图,现有边长为a的正方形纸片1张、边长为b的正方形纸片2张,边长分别为a,b的长方形纸片3张,把它们拼成一个长方形.请利用此拼图中的面积关系,分解因式:a2+3ab+2b2=查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:《第2章 简单事件的概率》2010年整章同步练习(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com