
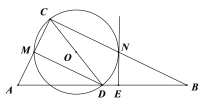
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC、BC相交于点M、N.
(1)过点N作⊙O的切线NE与AB相交于点E,求证:NE⊥AB;
(2)连接MD,求证:MD=NB.
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)如图,连接ON,根据直角三角形斜边中线等于斜边的一半可得AD=CD=DB,从而可得∠DCB=∠DBC,再由∠DCB=∠ONC,可推导得出ON∥AB,再结合NE是⊙O的切线,ON//AB,继而可得到结论;
(2)如图,由(1)可知ON∥AB,继而可得N为BC中点,根据圆周角定理可知∠CMD=90°,继而可得MD∥CB,再由D是AB的中点,根据得到MD=NB.
(1)如图,连接ON,
∵CD是Rt△ABC斜边AB上的中线,
∴AD=CD=DB,
∴∠DCB=∠DBC,
又∵OC=ON,∴∠DCB=∠ONC,
∴∠ONC=∠DBC,
∴ON∥AB,
∵NE是⊙O的切线,ON是⊙O的半径,
∴∠ONE=90°,
∴∠NEB=90°,即NE⊥AB;
(2)如图所示,由(1)可知ON∥AB,
∵OC=OD,∴
∴CN=NB=![]() CB,
CB,
又∵CD是⊙O的直径,∴∠CMD=90°,
∵∠ACB=90°,
∴∠CMD+∠ACB=180°,∴MD//BC,
又∵D是AB的中点,∴MD=![]() CB,
CB,
∴MD=NB.



 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A、B、C、D是正方形网格纸上的四个格点,根据要求在网格中画图并标注相关字母.
①画线段AB;
②画射线CA、直线AD;
③过点B画AD的平行线BE;
④过点D画AC的垂线,垂足为F.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了解政府调整水价方案的社会反响,随机访问了自己居住小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1、图2.

小明发现每月每户的用水量为5 ![]() -35
-35 ![]() 之间,有8户居民对用水价格调价涨幅抱无所谓,不会考虑用水方式的改变.根据小明绘制的图表和发现的信息,完成下列问题:
之间,有8户居民对用水价格调价涨幅抱无所谓,不会考虑用水方式的改变.根据小明绘制的图表和发现的信息,完成下列问题:
(1)![]() ,小明调查了 户居民,并补全图1;
,小明调查了 户居民,并补全图1;
(2)每月每户用水量的中位数和众数分别落在什么范围?
(3)如果小明所在小区有1800户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
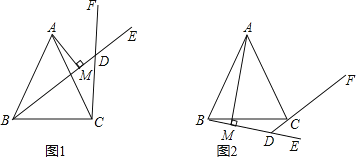
【题目】如图1,△ABC中,AB=AC,过B点作射线BE,过C点作射线CF,使∠ABE=∠ACF,且射线BE,CF交于点D,过A点作AM⊥BD于M.
(1)探究∠BDC和∠CAB的数量关系并说明理由;
(2)求证:BM=DM+DC;
(3)如图2,将射线BE,CF分别绕点B和点C顺时针旋转至如图位置,若∠ABE=∠ACF仍然成立,射线BE交射线CF的反向延长线于点D,过A点作AM⊥BD于M.请问(2)中的结论是否还成立?如果成立,请证明.如果不成立,线段BM,DM,DC又有怎样的数量关系?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
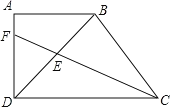
【题目】在四边形ABCD中,AB∥CD,∠A=90![]() ,AB=
,AB=![]() ,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△CDE的面积为_____.
,BD⊥BC,BD=BC,CF平分∠BCD交BD、AD于E、F,则△CDE的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线L:y=x2+x-6与x轴相交于A、B两点(点A在点B的左侧),并与y轴相交于点C.
(1)求A、B、C三点的坐标,并求出△ABC的面积;
(2)将抛物线向左或向右平移,得到抛物线L,且L与x轴相交于A、B两点(点A在点B的左侧),并与y轴交于点C,要使△ABC和△ABC的面积相等,求所有满足条件的抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号内:
-35,0.1,![]() ,0,
,0,![]() ,1,4.01001000···,22,-0.3,
,1,4.01001000···,22,-0.3,![]() ,
,![]() .
.
正数:{ ,···};
整数:{ ,···};
负分数:{ ,···};
非负整数:{ ,···}.
查看答案和解析>>
科目:初中数学 来源: 题型:
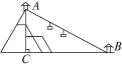
【题目】(1)喜欢爬山的同学都知道,很多名山上都有便于游人观光的索道,如图所示,山的高度AC为800 m,从山上A与山下B处各建一索道口,且BC=1 500 m,一游客从山下索道口坐缆车到山顶,知缆车每分钟走50 m,那么大约多长时间后该游客才能到达山顶?说明理由.
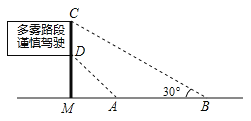
(2)如图,是矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,求警示牌的高度CD(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com