
 如图,是将抛物线y=-x2平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C.
如图,是将抛物线y=-x2平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0),另一个交点为B,与y轴的交点为C.分析 (1)已知抛物线的对称轴,因而可以设出顶点式,利用待定系数法求函数解析式;
(2)首先求得B和C的坐标,易证△OBC是等腰直角三角形,过点N作NH⊥y轴,垂足是H,设点N纵坐标是(a,-a2+2a+3),根据CH=NH即可列方程求解;
(3)四边形OAPQ是平行四边形,则PQ=OA=1,且PQ∥OA,设P(t,-t2+2t+3),代入y=$\frac{3}{2}$x+$\frac{3}{2}$,即可求解.
解答 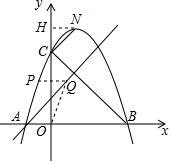 解:(1)设抛物线的解析式是y=-(x-1)2+k.
解:(1)设抛物线的解析式是y=-(x-1)2+k.
把(-1,0)代入得0=-(-1-1)2+k,
解得k=4,
则抛物线的解析式是y=-(x-1)2+4,即y=-x2+2x+3;
(2)在y=-x2+2x+3中令x=0,则y=3,即C的坐标是(0,3),OC=3.
∵B的坐标是(3,0),
∴OB=3,
∴OC=OB,则△OBC是等腰直角三角形.
∴∠OCB=45°,
过点N作NH⊥y轴,垂足是H.
∵∠NCB=90°,
∴∠NCH=45°,
∴NH=CH,
∴HO=OC+CH=3+CH=3+NH,
设点N坐标是(a,-a2+2a+3).
∴a+3=-a2+2a+3,
解得a=0(舍去)或a=1,
∴N的坐标是(1,4);
(3)∵四边形OAPQ是平行四边形,则PQ=OA=1,且PQ∥OA,
设P(t,-t2+2t+3),代入y=$\frac{3}{2}$x+$\frac{3}{2}$,则-t2+2t+3=$\frac{3}{2}$(t+1)+$\frac{3}{2}$,
整理,得2t2-t=0,
解得t=0或$\frac{1}{2}$.
∴-t2+2t+3的值为3或$\frac{15}{4}$.
∴P、Q的坐标是(0,3),(1,3)或($\frac{1}{2}$,$\frac{15}{4}$)、($\frac{3}{2}$,$\frac{15}{4}$).
点评 本题考查了待定系数法求二次函数解析式,以及等腰三角形、平行四边形的性质,注意到△OBC是等腰直角三角形是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 按一定规律组成的,其中第①个图形中一共有4颗
按一定规律组成的,其中第①个图形中一共有4颗 ,第②个图形中一共有11颗
,第②个图形中一共有11颗 ,第③个图形中一共有21颗
,第③个图形中一共有21颗 ,…,按此规律排列下去,第⑨个图形中
,…,按此规律排列下去,第⑨个图形中 的颗数为( )
的颗数为( )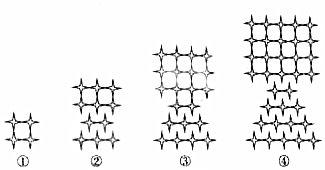
| A. | 116 | B. | 144 | C. | 145 | D. | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>1 | B. | k<1 | C. | k≥1 | D. | k≤1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在梯形ABCD中,AB∥DC,∠BCD=90°,且AB=2,BC=3,tan∠ADC=3.
如图,在梯形ABCD中,AB∥DC,∠BCD=90°,且AB=2,BC=3,tan∠ADC=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com