
【题目】已知:如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°.点D到地面的垂直距离![]() ,求点B到地面的垂直距离BC.
,求点B到地面的垂直距离BC.

科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
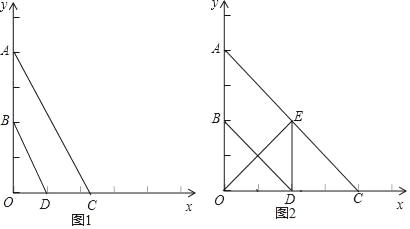
【题目】已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
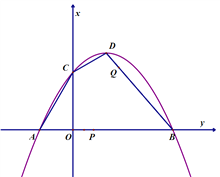
【题目】已知二次函数![]() 的图像如图,顶点坐标D为(3,
的图像如图,顶点坐标D为(3, ![]() )。它与
)。它与![]() 轴交于A,B两点(点A在B的左侧),与
轴交于A,B两点(点A在B的左侧),与![]() 轴交于C点,且AB的长为12. 动点P从A点出发,沿AB方向以1个单位长度/秒的速度向点B运动,设运动时间为t秒.
轴交于C点,且AB的长为12. 动点P从A点出发,沿AB方向以1个单位长度/秒的速度向点B运动,设运动时间为t秒.
(1)求二次函数的解析式;
(2)当△PDB为等腰三角形时,求t的值;
(3)若动点Q与P同时从A点出发,点Q沿折线ACCDDB运动,在AC,CD,DB上运动的速度分别为3,![]() ,2 (个单位长度/秒)﹒当P,Q中的一点到达B点时,两点同时停止运动.连结PQ.
,2 (个单位长度/秒)﹒当P,Q中的一点到达B点时,两点同时停止运动.连结PQ.
①当PQ的中点恰好落在y轴上时,求t的值;
②在P,Q的运动过程中,若线段PQ的垂直平分线与线段BD有交点时,请直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
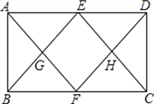
【题目】如图,在矩形ABCD中,E,F分别为AD,BC的中点,连结AF,DF,BE,CE,AF与BE交于G,DF与CE交于H.求证:四边形EGFH为菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
(1)求sinB的值;
(2)现需要加装支架DE、EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为点F,求支架DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程:(m﹣1)x2+(m﹣2)x﹣1=0(m为实数).
(1)若方程有两个不相等的实数根,求m的取值范围;
(2)若![]() 是此方程的实数根,抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B,抛物线的顶点为C,求△ABC的面积.
是此方程的实数根,抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B,抛物线的顶点为C,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com