
 如图,在平面直角坐标中,A点坐标为(0,4),B点坐标为(3,0),OD⊥AB于点D,试求D点的坐标.
如图,在平面直角坐标中,A点坐标为(0,4),B点坐标为(3,0),OD⊥AB于点D,试求D点的坐标. 分析 过D作DE⊥OB于E,由A点坐标为(0,4),B点坐标为(3,0),得到OA=4,OB=3,由勾股定理得到AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,根据三角形的面积公式得到OA•OB=AB•OD,求得OD=$\frac{12}{5}$,由射影定理得OD2=OE•OB,求得OE=$\frac{48}{25}$,即可得到结论.
解答 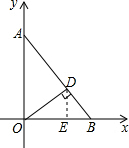 解:过D作DE⊥OB于E,
解:过D作DE⊥OB于E,
∵A点坐标为(0,4),B点坐标为(3,0),
∴OA=4,OB=3,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
∵OD⊥AB于点D,
∴OA•OB=AB•OD,
∴OD=$\frac{12}{5}$,
由射影定理得OD2=OE•OB,
∴OE=$\frac{48}{25}$,
∴DE=$\sqrt{O{D}^{2}-O{E}^{2}}$=$\frac{36}{25}$,
∴D($\frac{48}{25}$,$\frac{36}{25}$).
点评 本题考查了坐标与图形的性质,勾股定理,射影定理,三角形的面积.熟练掌握射影定理是解题的关键.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:选择题
| A. | 0的相反数是0,0的绝对值是0,同理0的倒数是0 | |
| B. | 因为ab=1,所以a和b都是倒数 | |
| C. | 因为ab=-1,所以a和b都是倒数 | |
| D. | -$\frac{5}{7}$和-$\frac{7}{5}$互为倒数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com