
����Ŀ����11�֣���ͼ���߳�Ϊ8��������OABC���������������ϣ��Ե�CΪ����������߾�����A����P���������ϵ�A��C���һ�����㣨���˵㣩������P��PF��BC�ڵ�F. ��D��E������ֱ�Ϊ��0��6������-4��0��������PD��PE��DE.

��1����ֱ��д�������ߵĽ���ʽ��
��2��С��̽����P��λ�÷��֣�����P���A���C�غ�ʱ��PD��PF�IJ�Ϊ��ֵ. �������룺��������һ��P��PD��PF�IJ�Ϊ��ֵ. �������ϸò����Ƿ���ȷ����˵�����ɣ�
��3��С����һ��̽���ó����ۣ�������ʹ��PDE�����Ϊ�������ĵ�P�������õ���������ڶ�����õ�������ʹ��PDE���ܳ���С�ĵ�PҲ��һ�����õ���.��ֱ��д���������õ����ĸ������������PDE���ܳ���Сʱ���õ���������.
���𰸡���1��y=-![]()
![]() +8��
+8��
��2����ȷ�����ɲμ�������
��3�����õ���11������PDE���ܳ���Сʱ���õ��������꣨-4,6��.
��������
�����������1����Ϊ�����߶Գ�����y�ᣬ���Ը���A,C�����꼴��д������ʽ.��2��������һ��P�������ʾ����������ʾ��PD,PF�ij�����PD-PF��֤����3�������ʹ��PDE���ܳ���С�ĵ�P�����꣬��DE�Ƕ�ֵ������PE��PD�ĺ���С��������ó��Ľ���ת����PE��PF�Ĺ�ϵ�����ó�ʹ��PDE���ܳ���С�ĵ�P�����ꣻ���ҵ����õ����ĸ������Ȱ�������PDE�������ʾ�����������������ȥ����ֱ�������ε��������x��ȡֵ��Χȷ��S������ֵ�м������ټ���ǰ���ʹ��PDE���ܳ���С��һ���㣬��֪��һ�����õ����ĸ���.
�����������1����y=a![]() +8����A��-8,0�����룬a=-
+8����A��-8,0�����룬a=-![]() ,��y=-
,��y=-![]()
![]() +8��
+8��
��2����P��x,-![]()
![]() +8��,��PF=8����-
+8��,��PF=8����-![]()
![]() +8��=
+8��=![]()
![]() ,��P��PM��y����M��
,��P��PM��y����M��
��![]() =
= =
=![]() ��
��
��PD=![]()
![]() +2����PD-PF=
+2����PD-PF=![]()
![]() +2��
+2��![]()
![]() =2����������ȷ.
=2����������ȷ.
��3������P���˶�ʱ��DE��С���䣬��PE��PD�ĺ���Сʱ����PDE���ܳ���С����PD-PF=2����PD=PF��2����PE��PD=PE��PF��2����P,E,F���㹲��ʱ��PE��PF��С����ʱ����P,E�����궼Ϊ-4����x=-4����y=-![]()
![]() +8����y=6,��P��-4,6��,��ʱ��PDE���ܳ���С������PDE�����Ϊ12����PǡΪ���õ��������PDE���ܳ���Сʱ���õ��������꣨-4,6��.����PH��AO��H,��PDE�����S=����PHOD�����ȥ����ֱ����������PHE,��DEO�����=-
+8����y=6,��P��-4,6��,��ʱ��PDE���ܳ���С������PDE�����Ϊ12����PǡΪ���õ��������PDE���ܳ���Сʱ���õ��������꣨-4,6��.����PH��AO��H,��PDE�����S=����PHOD�����ȥ����ֱ����������PHE,��DEO�����=-![]()
![]() ��3x��4=��
��3x��4=��![]()
![]() +13����-8��x��0֪4��S��13����S����������10������S=12ʱ����Ӧ�����õ�����1�����������õ�������11��.
+13����-8��x��0֪4��S��13����S����������10������S=12ʱ����Ӧ�����õ�����1�����������õ�������11��.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ȫ��ѧ�����������У������12����Ա������������£�
���䣨��λ���꣩ | 14 | 15 | 16 | 17 | 18 |
�ˡ��� | 1 | 4 | 3 | 2 | 2 |
��1������Ӷ�Ա���������������������������λ������������������
��2��������Ӷ�Ա��ƽ�����䣻
��3����������Ӷ�Ա����������ͳ��ͼ�����������Ϊ15���Ӧ��Բ�ĽǵĶ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��AB��DE��AC��DF��AC=DF�����������������ж���ABC�ա�DEF������������

A. AB=DE B. ��B=��E C. EF=BC D. EF��BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
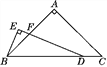
����Ŀ����ͼ����ABC�У�AB��AC����BAC��90�㣬��D���߶�BC�ϣ���EDB��![]() ��C��BE��DE������ΪE��DE��AB�ཻ�ڵ�F.��̽���߶�BE��DF��������ϵ����֤����Ľ��ۣ�
��C��BE��DE������ΪE��DE��AB�ཻ�ڵ�F.��̽���߶�BE��DF��������ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У��뾶Ϊ1����AԲ����ԭ��O�غϣ�ֱ��l�ֱ�x�ᡢy���ڵ�B��C������B������Ϊ(6��0)��tan��ABC=![]() ��
��

��1������P����A �ϵĶ��㣬��P��ֱ��BC����С���룬�����ʱ��P�����ꣻ
��2������A��ԭ��O��������1����λ/����ٶ�������·OB��BC��CO�˶����ص���Oֹͣ�˶�����A���ŵ�A���˶����ƶ������A�˶���ʱ��Ϊt��
������A�������˶�������������������ʱt��ȡֵ��
������A�������˶���������ɨ����ͼ�ε����Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е��鷽ʽ�����ʺ�ʹ��ȫ�������ǣ�������
A. �ÿ��Ϸɻ�ǰ�İ���B. ����ɻ�����ǰ�İ���
C. �˽�ȫ��ѧ��������D. �˽���������ѧ��ÿ��ʹ���ֻ���ʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������̻�������˾�����Ƴ���У�̻�����������շѷ���.
��˾������ÿ�µ���������y��Ԫ�����̻����x��ƽ���ף���һ�κ�����ϵ����ͼ��ʾ.
�ҹ�˾�������̻����������1000ƽ����ʱ��ÿ����ȡ����5500Ԫ���̻��������1000ƽ����ʱ��ÿ������ȡ5500Ԫ�Ļ����ϣ���������ÿƽ������ȡ4Ԫ.

��1������ͼ��ʾ��y��x�ĺ�������ʽ������Ҫ��дȡֵ��Χ��
��2�����ijѧУĿǰ���̻������1200ƽ����.��ͨ������˵����ѡ���ļҹ�˾�ķ���ÿ�µ��̻��������ý���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com