
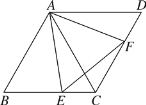
【题目】如图,△ABC和△ACD均为等边三角形,E是BC上的一个动点,F是CD上的一个动点,且∠EAF=60°.
(1)请判断△AEF的形状,并说明理由;
(2)当AB=4时,求△AEF面积的最小值.
【答案】(1)见解析;(2)3![]() .
.
【解析】(1)由等边三角形的性质得到AD=AC,∠D=∠ACB=60°,∠BAC=∠CAD=60°.再由∠EAF=60°,得到∠EAC=∠FAD.即可证明△AEC≌△AFD,由全等三角形的性质得到AE=AF,即可得到△AEF是等边三角形.
(2)由△AEF为等边三角形,得到S△AEF=![]() AE2.要使S△AEF最小,则需使AE最小,当AE⊥BC时,AE最小.求出AE的最小值,代入计算即可.
AE2.要使S△AEF最小,则需使AE最小,当AE⊥BC时,AE最小.求出AE的最小值,代入计算即可.
(1)△AEF是等边三角形.理由如下:
∵△ABC和△ACD均为等边三角形,∴AD=AC,∠D=∠ACB=60°,∠BAC=∠CAD=60°.
又∵∠EAF=60°,∴∠EAC=∠FAD.在△AEC与△AFD中,∵∠EAC=∠FAD,AC=AD,∠ACE=∠D,∴△AEC≌△AFD(ASA),∴AE=AF.
又∵∠EAF=60°,∴△AEF是等边三角形.
(2)由(1)知△AEF为等边三角形,∴S△AEF=![]() AE2.要使S△AEF最小,则需使AE最小,当AE⊥BC时,AE最小.此时.在Rt△ABE中,∵AB=4,∠B=60°,∴∠BAE=30°,∴BE=
AE2.要使S△AEF最小,则需使AE最小,当AE⊥BC时,AE最小.此时.在Rt△ABE中,∵AB=4,∠B=60°,∴∠BAE=30°,∴BE=![]() AB=2,∴AE=
AB=2,∴AE=![]() .∴S△AEF的最小值为
.∴S△AEF的最小值为![]() ×(
×(![]() )2=
)2=![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
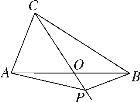
【题目】(题文)如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为________________(提示:直角三角形斜边上的中线等于斜边的一半).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某计算装置有一數据输入口A和一运算结果的输出口B,表格中是小明输入的一些数据和这些数据经该装置计算后输出的相应结果,按照这个计算装置的计算规律,若输入的数是10,则输出的数是( )
A | 1 | 2 | 3 | 4 | 5 |
B | 0 | 3 | 8 | 15 | 24 |
A. 99 B. 100 C. 101 D. 102
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一节数学活动课上,王老师将本班学生身高数据(精确到1厘米)出示给大家,要求同学们各自独立绘制一幅频数分布直方图,甲绘制的如图①所示,乙绘制的如图②所示,经王老师批改,甲绘制的图是正确的,乙在数据整理与绘图过程中均有个别错误.
(1)写出乙同学在数据整理或绘图过程中的错误(写出一个即可); 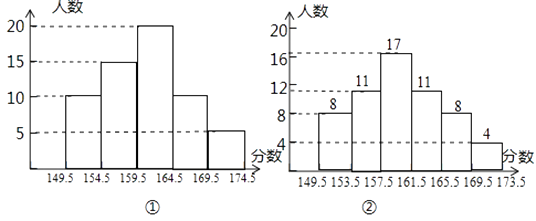
(2)甲同学在数据整理后若用扇形统计图表示,则159.5﹣164.5这一部分所对应的扇形圆心角的度数为;
(3)该班学生的身高数据的中位数是;
(4)假设身高在169.5﹣174.5范围的5名同学中,有2名女同学,班主任老师想在这5名同学中选出2名同学作为本班的正、副旗手,那么恰好选中一名男同学和一名女同学当正,副旗手的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金秋十月,长沙市某中学组织七年级学生去某综合实践基地进行秋季社会实践活动,每人需购买一张门票,该综合实践基地的门票价格为每张240元,如果一次购买500张以上(不含500张)门票,则门票价格为每张220元,请回答下列问题:
(1)列式表示n个人参加秋季社会实践活动所需钱数;
(2)某校用132000元可以购买多少张门票;
(3)如果我校490人参加秋季社会实践,怎样购买门票花钱最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面一组数:﹣1,2,﹣3,4,﹣5,6,﹣7,…,将这组数排成如图的形式,
第一行 -1
第二行 2 -3 4
第三行 -5 6 -7 8 -9
第四行 10 -11 12 -13 14 -15 16
按照如图规律排下去,(1)第10行中从左边数第4个数是__________;(2)前7行的数字总和是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )

A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
查看答案和解析>>
科目:初中数学 来源: 题型:
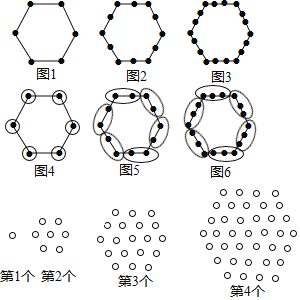
【题目】“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
例如:图1有6个点,图2有12个点,图3有18个点,……,按此规律,求图10、图n有多少个点?
我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;所以容易求出图10、图n中黑点的个数分别是 、 .
请你参考以上“分块计数法”,先将下面的点阵进行分块(画在答题卡上),再完成以下问题:
(1)第5个点阵中有 个圆圈;第n个点阵中有 个圆圈.
(2)小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种进价为20元/台的台灯,经调查发现,该台灯每天的销售量与销售单价基本满足一次函数关系,并且当销售单价为26元时,每天销售量28台;当销售单价为32元时,每天销售量16台,设台灯的销售单价为x(元),每天的销售量为y(台).
(1)求y与x之间的函数关系式;
(2)当销售单价定为多少元时,每天的利润最大?最大利润是多少?
(3)若该商场每天想获得150元的利润,在保证销售量尽可能大的前提下,应将销售单价定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com