
| A. | b<c<a | B. | a<c<b | C. | b<a<c | D. | c<b<a |
分析 根据乘法分配律可求a,将b变形为2015×2016-(2015-2)×(2016+2),再注意整体思想进行计算,根据提取公因式、平方差公式和算术平方根可求c,再比较大小即可求解.
解答 解:∵a=681×2019-681×2018
=681×(2019-2018)
=681×1
=681,
b=2015×2016-2013×2018
=2015×2016-(2015-2)×(2016+2)
=2015×2016-2015×2016-2×2015+2×2016+2×2
=-4030+4032+4
=6,
c=$\sqrt{67{8}^{2}+1358+690+678}$
=$\sqrt{678×(678+1)+679×2+690}$
=$\sqrt{679×(678+2)+690}$
=$\sqrt{680×680-680+690}$
=$\sqrt{680×680+2×680+1-1351}$
=$\sqrt{(680+1)^{2}-1351}$
=$\sqrt{68{1}^{2}-1351}$,
6<$\sqrt{68{1}^{2}-1351}$<681,
∴b<c<a.
故选:A.
点评 本题考查了因式分解的应用,熟记乘法分配律、平方差公式的结构特点是解题的关键.注意整体思想的运用.


科目:初中数学 来源: 题型:选择题
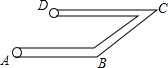 如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )| A. | AB∥BC | B. | BC∥CD | C. | AB∥DC | D. | AB与CD相交 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
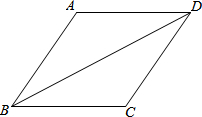 如图,在四边形ABCD中,∠BCD是钝角,AB=AD,BD平分∠ABC,若CD=3,BD=$2\sqrt{6}$,sin∠DBC=$\frac{{\sqrt{3}}}{3}$,求对角线AC的长.
如图,在四边形ABCD中,∠BCD是钝角,AB=AD,BD平分∠ABC,若CD=3,BD=$2\sqrt{6}$,sin∠DBC=$\frac{{\sqrt{3}}}{3}$,求对角线AC的长.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲乙两工程队同时修路,两队所修路的长度相等,甲队施工速度一直没变,乙队在修了3小时后加快了修路速度,在修了5小时后,乙又因故施工速度减少到每小时5米,如图所示是两队所修公路长度y(米)与所修时间x(小时)的图象,请回答下列问题.
甲乙两工程队同时修路,两队所修路的长度相等,甲队施工速度一直没变,乙队在修了3小时后加快了修路速度,在修了5小时后,乙又因故施工速度减少到每小时5米,如图所示是两队所修公路长度y(米)与所修时间x(小时)的图象,请回答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com