
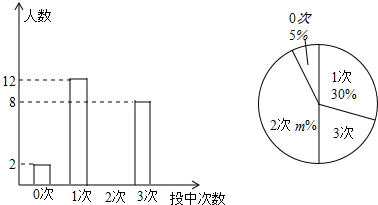
分析 (1)根据总数=频数÷百分比进行计算即可;利用总数减去投中0次,1次,3次的人数可得投中2次的人数,再根据百分比=频数÷总数×100%可得投中2次、3次的百分比,再补全图形即可;
(2)根据加权平均数、中位数、极差的定义计算即可;
(3)列出从2男、2女这4人中随机抽出3人可能产生的结果,根据概率公式计算即可得.
解答 解:(1)九年级(1)班学生人数:2÷5%=40(人);
投中两次的人数:40-2-12-8=18(人),m=18÷40×100=45,8÷40×100%=20%.
补全统计图如图: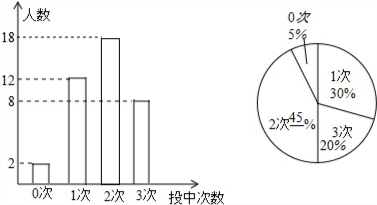
(2)平均数为:$\frac{0×2+1×12+2×18+3×8}{40}$=1.8(次),
中位数为:$\frac{2+2}{2}$=2(次),
极差为:3-0=3(次);
(3)将四名学生分别即为:男1、男2、女1、女2,
从这4人中随机抽出3人有:男1、男2、女1;男1、男2、女2;男1、女1、女2;男2、女1、女2,这4种等可能结果;
其中刚好是2名男生1名女生的结果有2种,
故从这4人中随机抽出3人,刚好是2名男生1名女生的概率为$\frac{2}{4}$=$\frac{1}{2}$.
故答案为:(1)40,45.
点评 此题主要考查了条形统计图和扇形统计图的综合运用及平均数、中位数、极差、概率的计算,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
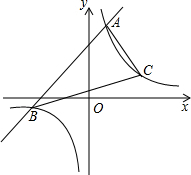 已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A,B两点,当x>1,时,y1>y2;当0<x<1时,y1<y2.
已知一次函数y1=x+m的图象与反比例函数y2=$\frac{6}{x}$的图象交于A,B两点,当x>1,时,y1>y2;当0<x<1时,y1<y2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
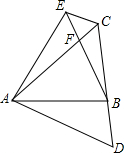 已知△ABC,将边AC绕点A顺时旋转60°得到AD,将AB绕点A逆时针旋转60°得到AE连接CD,CE,且点B在CD上
已知△ABC,将边AC绕点A顺时旋转60°得到AD,将AB绕点A逆时针旋转60°得到AE连接CD,CE,且点B在CD上查看答案和解析>>
科目:初中数学 来源: 题型:解答题
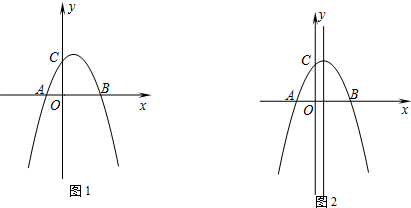
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
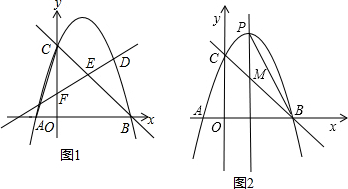
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
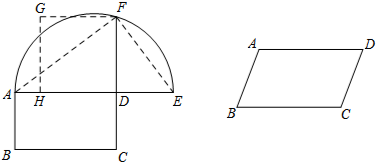
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A,B两点,且交y轴于点C.已知点A(1,4),点B在第三象限,且点B的横坐标为t(t<-1).
一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A,B两点,且交y轴于点C.已知点A(1,4),点B在第三象限,且点B的横坐标为t(t<-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com