
【题目】某家禽养殖场,用总长为110m的围栏靠墙(墙长为22m)围成如图所示的三块矩形区域,矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,设AD长为xm,矩形区域ABCD的面积为ym2.
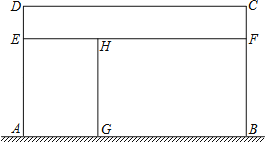
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,y有最大值?最大值是多少?
【答案】(1)y=﹣![]() x2+55x,自变量x的取值范围为:24≤x<40;(2)当x=24时,y有最大值,最大值为528平方米.
x2+55x,自变量x的取值范围为:24≤x<40;(2)当x=24时,y有最大值,最大值为528平方米.
【解析】
试题分析:(1)根据矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,得到矩形AEFB面积是矩形CDEF面积的3倍,求得AD=3DE,于是得到y=x(55﹣![]() x)=﹣
x)=﹣![]() x2+55x,自变量x的取值范围为:24≤x<40;
x2+55x,自变量x的取值范围为:24≤x<40;
(2)把y=﹣![]() x2+55x化为顶点式:y=﹣
x2+55x化为顶点式:y=﹣![]() ( x﹣20)2+550,根据二次函数的性质即可得到结论.
( x﹣20)2+550,根据二次函数的性质即可得到结论.
解:(1)∵矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,
∴矩形AEFB面积是矩形CDEF面积的3倍,
∴AD=3DE,
∵AD=x,
∴GH=![]() x,
x,
∵围栏总长为110m,
∴2x+![]() x+2CD=110,
x+2CD=110,
∴CD=55﹣![]() x,
x,
∴y=x(55﹣![]() x)=﹣
x)=﹣![]() x2+55x,
x2+55x,
∴自变量x的取值范围为:24≤x<40;
(2)∵y=﹣![]() x2+55x=﹣
x2+55x=﹣![]() ( x2﹣40 x)=﹣
( x2﹣40 x)=﹣![]() ( x﹣20)2+550,
( x﹣20)2+550,
∵自变量x的取值范围为:24≤x<40,且二次项系数为﹣![]() <0,
<0,
∴当x=24时,y有最大值,最大值为528平方米.


科目:初中数学 来源: 题型:
【题目】有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.现要把它加工成矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB,AC上.
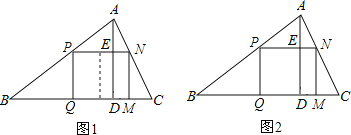
(1)如果此矩形可分割成两个并排放置的正方形,如图1,此时,这个矩形零件的两条邻边长分别为多少mm?请你计算.
(2)如果题中所要加工的零件只是矩形,如图2,这样,此矩形零件的两条邻边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条邻边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).
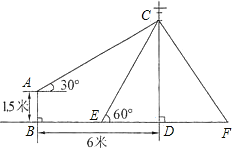
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,矩形ABCD的对角线相交于点O,
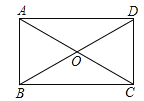
(1)若AB=2,∠AOD=120,求对角线AC的长;
(2)若AC=2AB.求证:△AOB是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
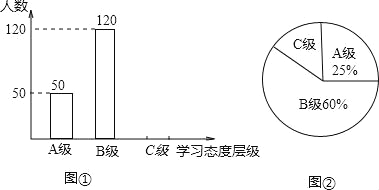
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在作二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象时,先列出下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y1 | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 | … |
y2 | … | 0 | 2 | 4 | 6 | 8 | 10 | 12 | … |
请你根据表格信息回答下列问题,
(1)二次函数y1=ax2+bx+c的图象与y轴交点坐标为 ;
(2)当y1>y2时,自变量x的取值范围是 ;
(3)请写出二次函数y1=ax2+bx+c的三条不同的性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
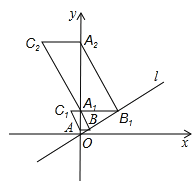
【题目】如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1,以A1B、BA为邻边作□ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作□A1B1A2C2…;按此作法继续下去,则Cn的坐标( )
A.(﹣![]() ×4n,4n) B.(﹣
×4n,4n) B.(﹣![]() ×4n-1,4n-1)
×4n-1,4n-1)
C.(﹣![]() ×4n﹣1,4n) D.(﹣
×4n﹣1,4n) D.(﹣![]() ×4n,4n-1)
×4n,4n-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com