
分析 设鸡场的宽为x米,则长为(x+5)米或(x+2)米,根据篱笆的长为5米即可得出关于x的一元一次方程,解之即可求出x值,再结合养鸡场的长不超过14米即可确定小王和小华建议的长方形的长和宽,利用长方形的面积公式分别求出两人建议的长方形的面积,比较后即可得出结论.
解答 解:设鸡场的宽为x米,则长为(x+5)米或(x+2)米,
根据题意得:2x+x+5=35或2x+x+2=35,
解得:x=10或x=11.
当x=10时,x+5=15>14,
∴依小王的检验,鸡场的长为14米,宽为9米,
此时鸡场的面积S=14×9=126(平方米);
当x=11时,x+2=13,
∴依小华的建议,鸡场的长为13米,宽为11米,
此时鸡场的面积S=13×11=143(平方米).
∵126<143,
∴小华的建议符合实际,按照他的建议,鸡场的面积是143平方米.
点评 本题考查了一元一次方程的应用,根据篱笆的长为5米列出关于x的一元一次方程是解题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
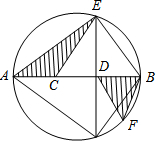 如图,半径为3cm的⊙O中,C,D为直径AB的三等分点,点E,F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连接AE,BF,则图中两个阴影部分的面积为$\frac{3\sqrt{11}}{2}$.
如图,半径为3cm的⊙O中,C,D为直径AB的三等分点,点E,F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连接AE,BF,则图中两个阴影部分的面积为$\frac{3\sqrt{11}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
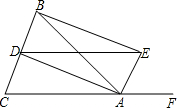 如图,在△ABC中,AB=AC,AD、AE分别是∠BAC和∠BAF的平分线,BE⊥AE
如图,在△ABC中,AB=AC,AD、AE分别是∠BAC和∠BAF的平分线,BE⊥AE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com